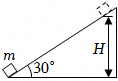
如图所示，一固定斜面的倾角为$30^\circ$，一质量为$m$的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动，加速度大小等于$0.8g$（$g$为重力加速度大小），物块上升的最大高度为$H$，则此过程中$(\qquad)$

物块的重力做功$mgH$

物块的动能损失了$mgH$

物块的机械能损失了$0.6mgH$

物块克服摩擦力做功$1.6mgH$

$\rm A$、物块上升的最大高度为$H$，重力做功为：$W_{G}=-mgH$，故$\rm A$错误；

$\rm B$、由牛顿第二定律可得物块所受合力大小为：$F_{合}=ma=m\times 0.8g=0.8mg$

由几何关系可得物体沿斜面运动的位移为：$x=2H$

物块上升到最高点过程，由动能定理可得物块损失的动能为：$\Delta E_{k}=F_{合}x=0.8mg\cdot 2H=1.6mgH$，故$\rm B$错误；

$\rm CD$、对物块由牛顿第二定律有：$mg\sin30^\circ+f=ma$，可得物块所受摩擦力为：$f=0.3mg$，则物块克服摩擦力做的功为：$W_{f}=fx=0.3mg\cdot 2H=0.6mgH$

根据功能关系可知物块机械能损失量等于克服摩擦力做的功，即：$\Delta E=W_{f}=0.6mgH$，故$\rm C$正确，$\rm D$错误。

故选：$\rm C$。