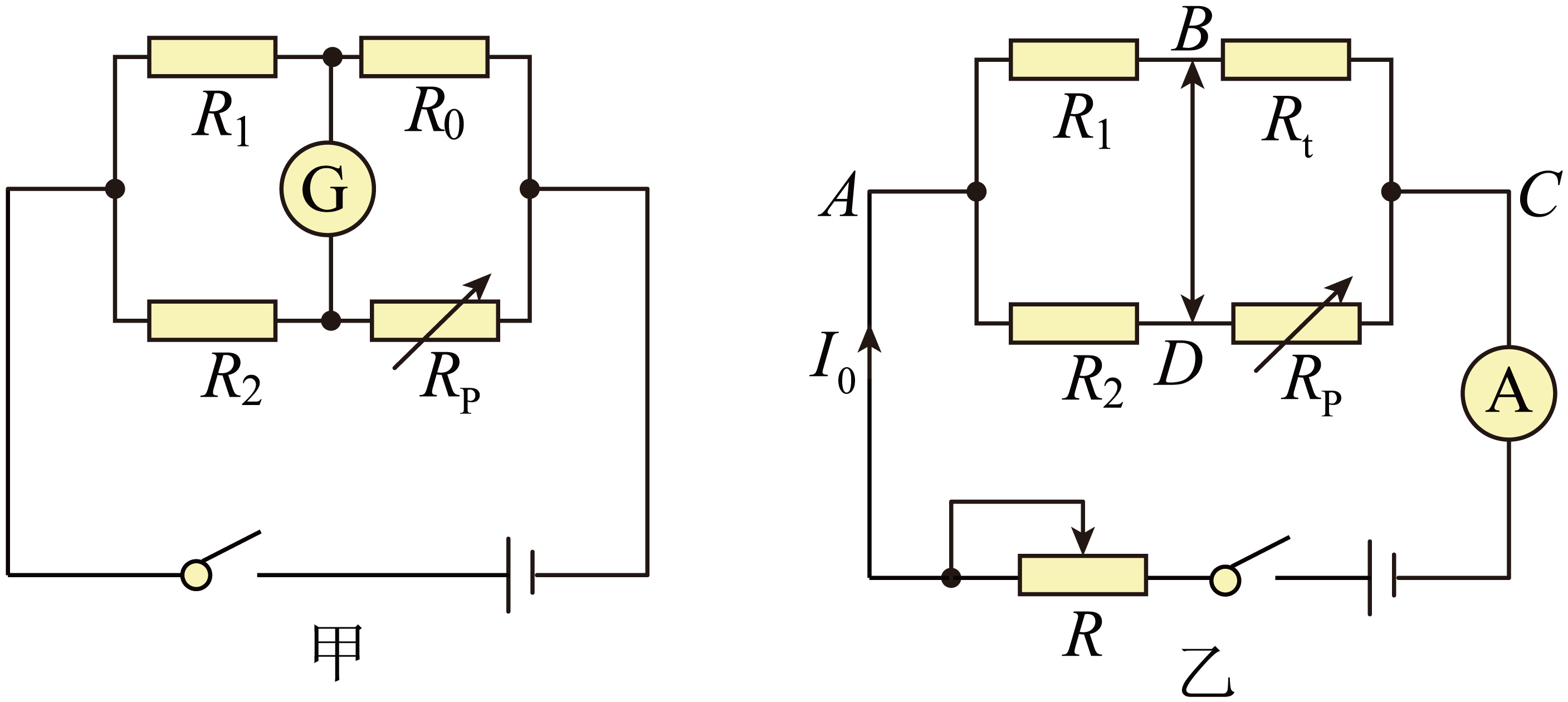
他们利用图甲所示电路来测量$R_{0}$的阻值，其中定值电阻$R_{1}=R_{2}$且远大于$R_{t}$和$R_{p}$，按图甲连接好电路后，在$0^\circ\rm C$的条件下闭合开关$\rm S$，调节电阻箱$R_{p}$，当$R_{p}=50.0\;\rm \Omega$时灵敏电流计$G$的示数为零，则$R_{0}=$                 $\;\rm \Omega$；

在$0^\circ\rm C$的条件下闭合开关$\rm S$，调节电阻箱$R_{p}$，当$R_{\rm p}=50.0\;\rm \Omega$时灵敏电流计$G$的示数为零，则$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{0}}{R_{{p}}}$

解得$R_{0}=50\Omega$。

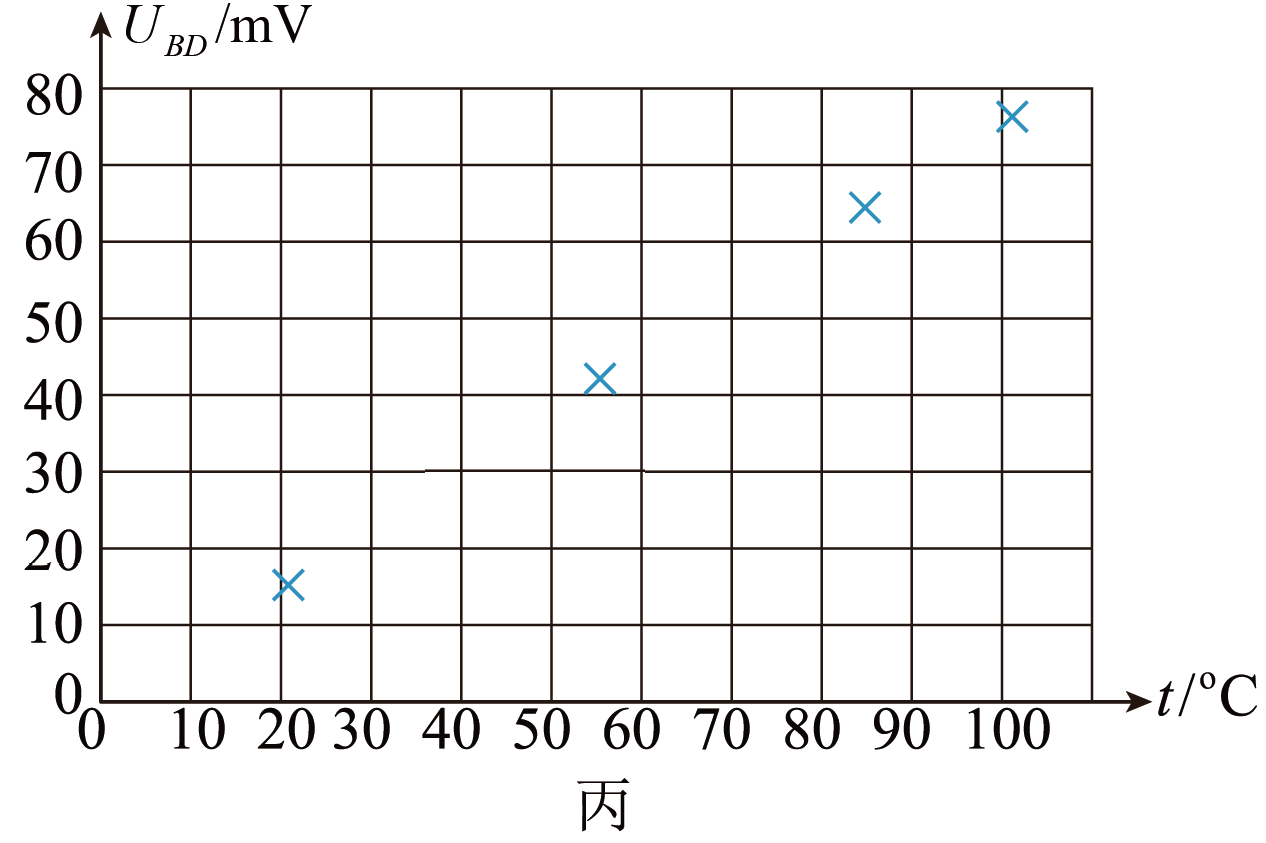
他们随后用图乙电路测量铂电阻的温度系数，其中定值电阻$R_{1}=R_{2}$且远大于$R_{t}$和$R_{p}$，将铂电阻置于温度为$t$的环境中，调节$R_{ p}=R_{0}$，测得干路电流为$I_{0}=3.00\;\rm mA$，则图乙中$B$、$D$两点间的电压为$U_{BD}=$                 （用$I_{0}$、$R_{0}$、$t$和$\alpha$表示）；多次改变温度$t$，保持$R_{\rm p}=R_{0}$不变，调节滑动变阻器，使得电流表示数保持为$I_{0}$不变，测量$B$、$D$两点间的电压$U_{BD}$，将测得的数据标在图丙所示的$U_{BD} − t$图上，由此可得$\alpha=$                 $^\circ\rm C^{-1}$（保留两位有效数字）；

由于定值电阻$R_{1}=R_{2}$且远大于$R_{t}$和$R_{ p}$，调节$R_{p}=R_{0}$，则流过$R_{1}$、$R_{2}$的电流均为$\dfrac{1}{2}I_{0}$，则有$U_{BC}=\dfrac{1}{2}I_{0}R_{0}(1+\alpha t)$

$U_{DC}=\dfrac{1}{2}I_{0}R_{0}$

解得$U_{BD}=U_{BC}-U_{DC}=\dfrac{1}{2}I_{0}R_{0}\alpha t$

将用一条倾斜的直线将图丙补充完整，如下图所示

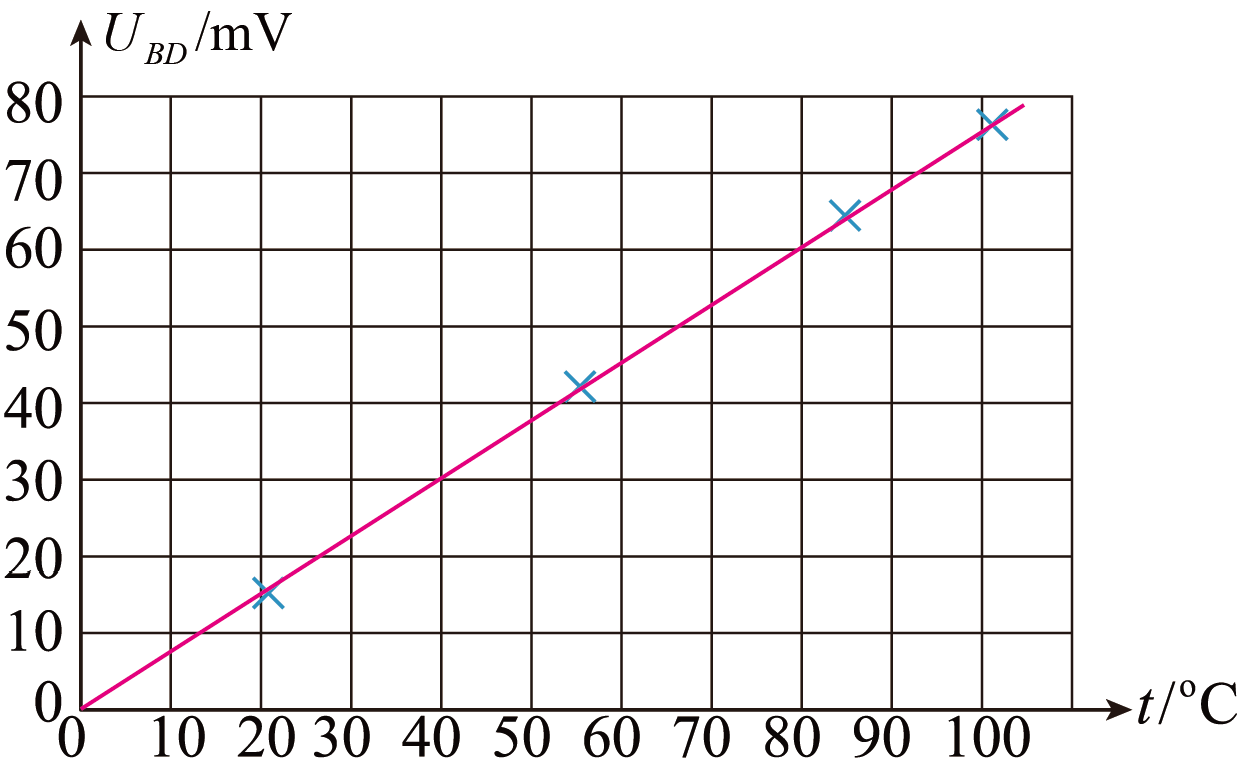
根据图像斜率结合$U_{BD}=\dfrac{1}{2}I_{0}R_{0}\alpha t$可知

$k=\dfrac{1}{2}I_{0}R_{0}\alpha=\dfrac{75\;\text{mV}}{100\;{^\circ}\text{C}}$

解得$\alpha=0.01\;^\circ\rm C^{-1}$。

上述实验过程中，非常强调“定值电阻$R_{1}=R_{2}$且远大于$R_{t}$和$R_{p}$”，请分析指出，为什么要保证“远大于”这一限制条件：                。

见解析

若实验中没有保证$R_{1}$、$R_{2}$远大于$R_{t}$、$R_{\rm p}$，则通过$R_{1}$的电流小于通过$R_{2}$的电流，则

$U_{BC} \lt \dfrac{1}{2}I_{0}R_{0}(1+\alpha t)$，$U_{DC} \gt \dfrac{1}{2}I_{0}R_{0}$

导致$U_{BD} \lt \dfrac{1}{2}I_{0}R_{0}\alpha t$

则有故导致温度系数的测量值偏小。