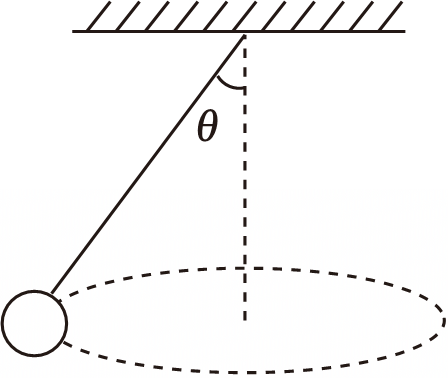
如图所示，小球（视为质点）用细线悬于天花板上，使小球在水平面内做匀速圆周运动，悬线与竖直方向的夹角为$\theta$，小球做圆周运动的周期为$T$，重力加速度为$g$，则悬线的长度为$(\qquad)$

$\\dfrac{T^{2}g}{4\\pi^{2}\\cos\\theta}$

$\\dfrac{T^{2}g}{4\\pi^{2}\\sin\\theta}$

$\\dfrac{T^{2}g}{4\\pi^{2}}$$\\cos\\theta$

$\\dfrac{T^{2}g}{4\\pi^{2}}$$\\sin\\theta$

设悬线的长度为$L$，悬线拉力和小球重力的合力提供向心力，根据牛顿第二定律，有$mg\tan\theta=mL\sin\theta\cdot \dfrac{4\pi^{2}}{T^{2}}$，解得$L= \dfrac{gT^{2}}{4\pi^{2}\cos\theta}$，故$\rm A$正确，$\rm BCD$错误。

故选：$\rm A$。