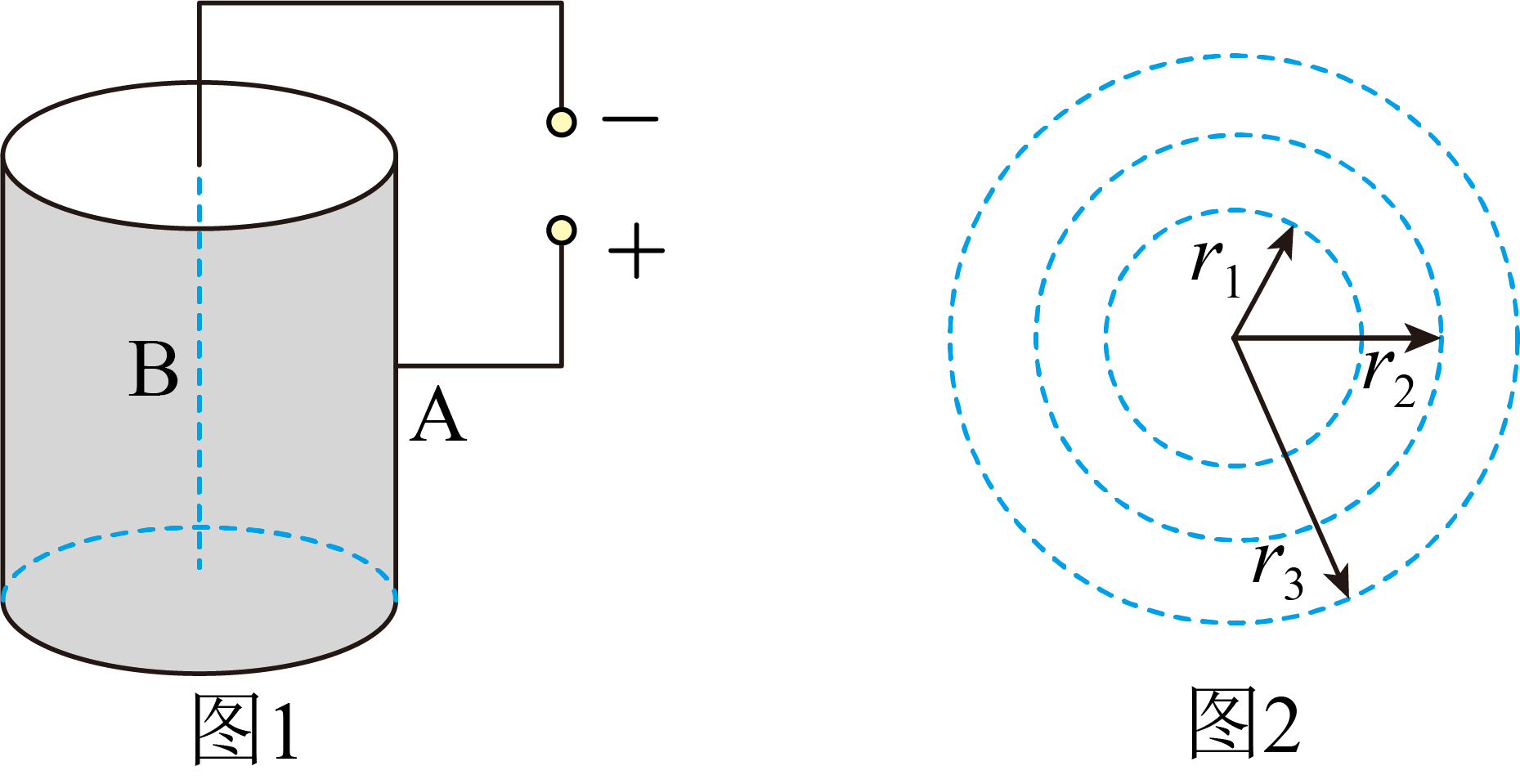
设$A$、$B$两极间电压为$U$，求在$B$极附近电荷量为$Q$的负电荷到达$A$极过程中静电力做的功$W$；

$W=QU$；

在$B$极附近电荷量为$Q$的负电荷到达$A$极过程中静电力做的功$W=−Q ⋅ (−U)=QU$；

已知筒内距离轴线$r$处的电场强度大小$E= k\dfrac{2\lambda}{r}$，其中$k$为静电力常量，$\lambda$为金属线$B$单位长度的电荷量。如图$2$所示，在圆筒内横截面上，电荷量为$q$、质量为$m$的粒子绕轴线做半径不同的匀速圆周运动，其半径为$r_{1}$、$r_{2}$和$r_{3}$时的总能量分别为$E_{1}$、$E_{2}$和$E_{3}$。若$r_{3} − r_{2}=r_{2} − r_{1}$，推理分析并比较$(E_{3} − E_{2})$与$(E_{2} − E_{1})$的大小；

$(E_{3} − E_{2}) \\lt (E_{2} − E_{1})$；

粒子在半径为$r$处绕轴线做匀速圆周运动，其向心力由电场力提供，根据向心力公式$qE=m\dfrac{v^{2}}{r}$

又$E=k\dfrac{2\lambda}{r}$

联立可得$qk\dfrac{2\lambda}{r}=m\dfrac{v^{2}}{r}$

解得粒子的动能$E_{\rm{k}}=\dfrac{1}{2}mv^{2}=qk\lambda$

设无穷远处电势能为$0$，粒子从无穷远处移动到半径为$r$处，电场力做功$W=q∫_{∞}^{r}Edr$

其中$E=k\dfrac{2\lambda}{r}$

代入可得$W=q\int_{\infty}^{r}{}k\dfrac{2\lambda}{r}{d}r=- 2qk\lambda\ln r$

根据$W=−\Delta E_\rm{p}$

可得粒子在半径为$r$处的电势能$E_{\rm p}=2qk\lambda\ln r$

粒子的总能量粒子的总能量$E=E_{\rm k}+E_{\rm p}=qk\lambda+2qk\lambda\ln r$

则$E_{3} − E_{2}=2qk\lambda(\ln r_{3} − r_{2})$，$E_{2} − E_{1}=2qk\lambda(\ln r_{2} − r_{1})$

根据数学知识可知对数函数$y=\ln x$在（$0$，$∞$）是增函数，且$\ln x$的二阶导数$\left( \ln x \right)''=- \dfrac{1}{x^{2}} \lt 0$

所以$y=\ln x$是凹函数，已知$r_{3} − r_{2}=r_{2} − r_{1}$，即$r_{2}$是$r_{1}$与$r_{3}$的等差中项，根据凹函数的性质$\ln r_{2} \gt \dfrac{\ln r_{1}+\ln r_{3}}{2}$

移项可得$\ln r_{3} − \ln r_{2} \lt \ln r_{2} − \ln r_{1}$

又因为$2qk\lambda \gt 0$

可得$(E_{3} − E_{2}) \lt (E_{2} − E_{1})$；

图$1$实为某种静电除尘装置原理图，空气分子在$B$极附近电离，筒内尘埃吸附电子而带负电，在电场作用下最终被$A$极收集。使分子或原子电离需要一定条件。以电离氢原子为例。根据玻尔原子模型，定态氢原子中电子在特定轨道上绕核做圆周运动，处于特定能量状态，只有当原子获得合适能量才能跃迁或电离。若氢原子处于外电场中，推导说明外电场的电场强度多大能将基态氢原子电离。（可能用到：元电荷$e=1.6 \times 10^{-19}\;\rm C$，电子质量$m=9.1 \times 10^{-31}\;\rm kg$，静电力常量$k=9.0 \times 10^{9}\;\rm N ⋅ m^{2}/C^{2}$，基态氢原子轨道半径$a=5.3 \times 10^{-11}\;\rm m$和能量$E_{0}=-13.6\;\rm eV$）

$E ≈ 2.57 \\times 10^{11}\\;\\rm N/C$。

方法一：电子绕核做圆周运动，库仑力提供向心力，即$k\dfrac{e^{2}}{a^{2}}=m\dfrac{v^{2}}{a}$

电子的动能$E_{\rm{k}}=\dfrac{1}{2}mv^{2}$

联立可得$E_{\rm{k}}=\dfrac{ke^{2}}{2a}$

根据库仑定律，电子与原子核之间的库仑力$F=k\dfrac{e^{2}}{a^{2}}$

电子从基态轨道半径$a$处运动到无穷远处，克服库仑力做功$W_{库}=\int_{a}^{\infty}\dfrac{ke^{2}}{r^{2}}\text{d}r$

积分可得$W_{库}=\dfrac{ke^{2}}{a}$

则电子在基态轨道半径$a$处的电势能$E_{\rm p}=−W_{库}$

根据能量守恒定律，将基态氢原子电离所需的能量$\Delta E$等于电子的动能与基态氢原子的势能之和，即$\Delta E=E_{\rm{k}}+E_{\rm{p}}=\dfrac{ke^{2}}{2a}$

设外电场的电场强度为$E$，电子在电场力作用下获得能量，当电子获得的能量等于将基态氢原子电离所需的能量时，氢原子被电离。电子在电场力作用下获得的能量$W=\Delta E=eEa$

联立可得$E=\dfrac{ke}{2a^{2}}$

代入数据解得$E ≈ 2.57 \times 10^{11}\;\rm N/C$

方法二：根据功能关系可得$eEa=|E_{0}|$

代入数据可得$E ≈ 2.57 \times 10^{11}\;\rm N/C$。