在纸面上有两波源$S_{1}$和$S_{2}$相距$3\;\rm m$，频率均为$2\;\rm Hz$，以$S_{1}$为原点建立如图所示的坐标系，$t=0$时波源$S_{1}$从平衡位置开始垂直纸面向上做简谐运动，所激发的横波在均匀介质中向四周传播。$t=0.25\;\rm s$时波源$S_{2}$也开始垂直纸面向上做简谐运动，在$t=0.75\;\rm s$时两列简谐波的最远波峰传到了图示中的两个圆的位置。则$(\qquad)$

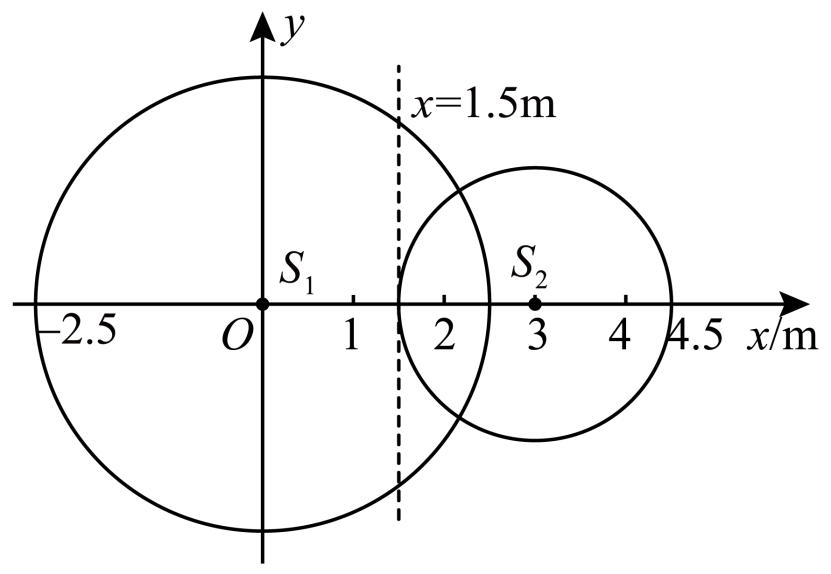
波的传播速度为$4\\;\\rm m/s$

虚线$x=1.5\\;\\rm m$为振动加强区

$t=1.0\\;\\rm s$时波谷与波谷相遇的点共有$2$个

$t=1.0\\;\\rm s$后$S_{1}$和$S_{2}$连线上有$2$个振动减弱的位置

$\rm A$．两波源起振的时间差为$\Delta t=0.25\;\rm s$

$\Delta t$时间内两列波的传播距离之差为$\Delta x=2.5\;\rm m-1.5\;\rm m=1\;\rm m$

波的传播速度为$v=\dfrac{\Delta x}{\Delta t}=4\;\rm \text{m/s}$

故$\rm A$正确；

$\rm B$．根据几何关系可知$x=1.5\;\rm m$上各质点到两波源的波程差均为零，而$t=0.25\;\rm s$时$S_{1}$正向下振动，与$S_{2}$起振方向相反，所以两波源在$x=1.5\;\rm m$上引起质点的振动步调相反，即虚线$x=1.5\;\rm m$为振动减弱区，故$\rm B$错误；

$\rm C$．两列波的波长均为$\lambda=\dfrac{v}{f}=2\;\rm \text{m}$

$t=1.0\;\rm s$时$S_{1}$波传播到的最远位置到$S_{1}$的距离为$d_{1}=2\lambda=4\;\rm m$

此时$S_{1}$波的最远波谷到$S_{1}$的距离为$r_{1}=d_{1}-\dfrac{3}{4}\lambda=2.5\;\rm \text{m}$

$S_{1}$波的最近波谷到$S_{1}$的距离为

$r_{1}'=r_{1}-\lambda=0.5\;\rm m$

$t=1.0\;\rm s$时$S_{2}$波传播到的最远位置到$S_{2}$的距离为

$d_{2}=\dfrac{3}{2}\lambda=3\;\rm \text{m}$

$S_{2}$波此时产生的波形中只有一个波谷，且到$S_{2}$的距离为$r_{2}=d_{2}-\dfrac{3}{4}\lambda=1.5\;\rm \text{m}$

如图所示，可知$t=1.0\;\rm s$时波谷与波谷相遇的点共有$2$个，故$\rm C$正确；

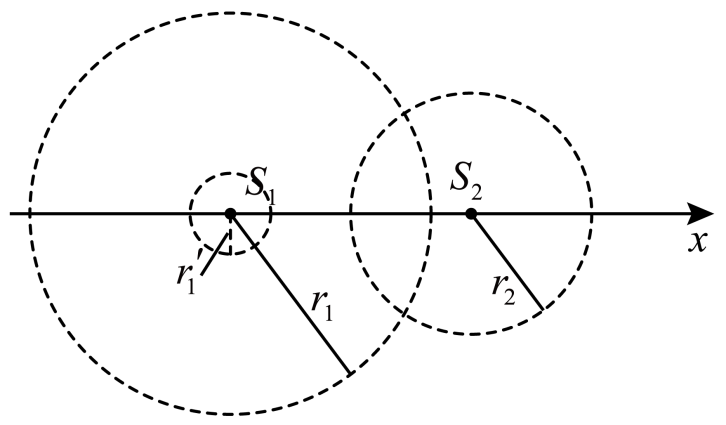
$\rm D$．$S_{1}$和$S_{2}$连线上满足到两波源的波程差为波长的整数倍的点为振动减弱位置，即

$\Delta s=|k\lambda|(k=0,1,2,…)$

则$0\lt |k\lambda|\lt 3\;{\rm m}(k=0,1,2,…)$

解得$- \dfrac{3}{2}\lt k\lt \dfrac{3}{2}(k=0,1,2,…)$

即$k=0, ±1$

所以$t=1.0\;\rm s$后$S_{1}$和$S_{2}$连线上有$3$个振动减弱的位置，故$\rm D$错误。

故选：$\rm AC$。