某水上游乐项目用固定在振动片上的细杆周期性地上下触动水面，在水面产生水波。以细杆浸入点为坐标原点，沿波在水面传播的某一方向建立$x$轴。图中的实线和虚线分别为$t=0$和$t=0.2\;\rm s$时的波形图。已知平衡位置在$x=2m$处的质点，在$t=0$时运动方向向上。由此可判断该波$(\qquad)$

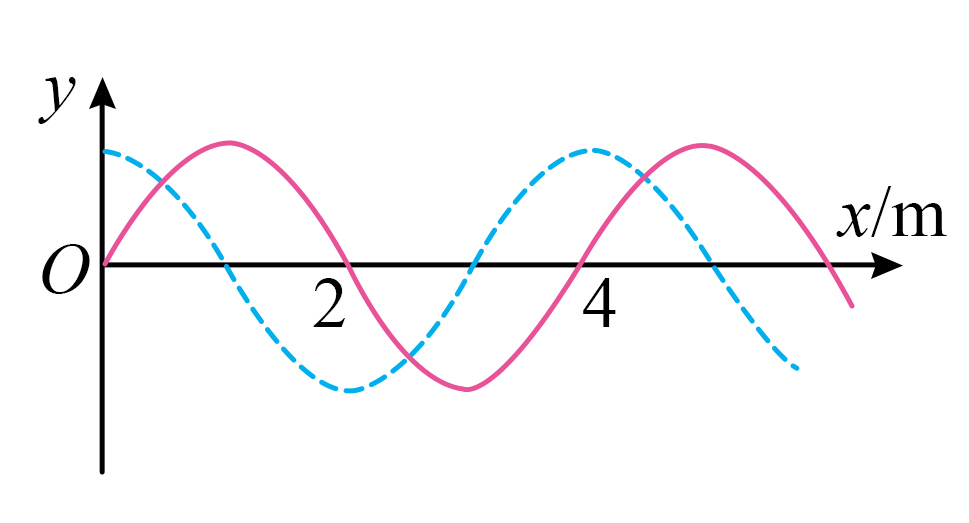
沿$x$轴正方向传播

沿$x$轴负方向传播

波速可能为$45\\;\\rm m/s$

波速可能为$55\\;\\rm m/s$

$\rm AB$．题意知平衡位置在$x=2m$处的质点，在$t=0$时运动方向向上。同侧法可知该波沿沿$x$轴正方向传播，故$\rm A$正确，$\rm B$错误；

$\rm CD$．波形可知，波长$\lambda=4m$，且$\Delta t=nT+\dfrac{3}{4}T=0.2\;\rm {s}（n=0,1,2,3\cdots )$，联立解得波速$v=\dfrac{3+4n}{0.2}\;\rm{m/s}$，则$n$取$0$时，波速为$15\;\rm m/s$，$n$取$1$时，波速为$35\;\rm m/s$，$n$取$2$时，波速为$55\;\rm m/s$，故$\rm C$错误，$\rm D$正确；

故选：$\rm AD$；

如图所示，小冲同学站在滑板上，初始时两者均处于静止状态。小冲水平向右抛出质量为$m_{1}$的沙包，抛出点离地高度为$h$，沙包落地点到抛出点的直线距离为$\sqrt{2}h$。已知小冲和滑板的总质量为$m_{2}$，忽略滑板与水平地面间的摩擦及空气阻力影响，重力加速度为$g$。则沙包水平抛出的速度大小为                 。沙包落地时，滑板向左滑行的距离为                 ；

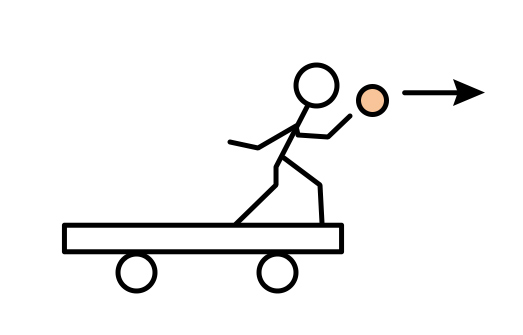
根据平抛运动规律有$h= \dfrac{1}{2}gt^{2}$，$\sqrt{{(\sqrt{2}h)}^{2}-h^{2}}=vt$

联立解得沙包水平抛出的速度大小$v=\sqrt{\dfrac{gh}{2}}$，$t=\sqrt{\dfrac{2h}{g}}$

对$m_{1}$、$m_{2}$，由动量守恒有$m_{1}v=m_{2}v_{2}$

因为沙包落地时，滑板向左滑行的距离$x_{2}=v_{2}t$

联立解得$x_{2}=\dfrac{m_{1}}{m_{2}}h$；

如图，小明同学骑自行车沿地面平直道路$A'B'$向左做匀减速直线运动，观景台上的摩天轮与$A'B'$在同一竖直平面内。摩天轮半径$R=60.0m$，其圆心$O$离地高度$h=180m$，轿厢绕$O$点顺时针匀速转动，周期$T=16.0\;\rm \min$。当摩天轮的一个轿厢在最低点$A$时小明恰好在其正下方$A'$点，小明相对此轿厢的速度大小$v=3.50\;\rm m/s$，方向水平向左；此轿厢运动到摩天轮上与$O$点在同一水平高度的$B$点时小明运动到$B'$点，小明相对此轿厢的速度方向恰好沿$BB'$连线且$B$指向$B'$。

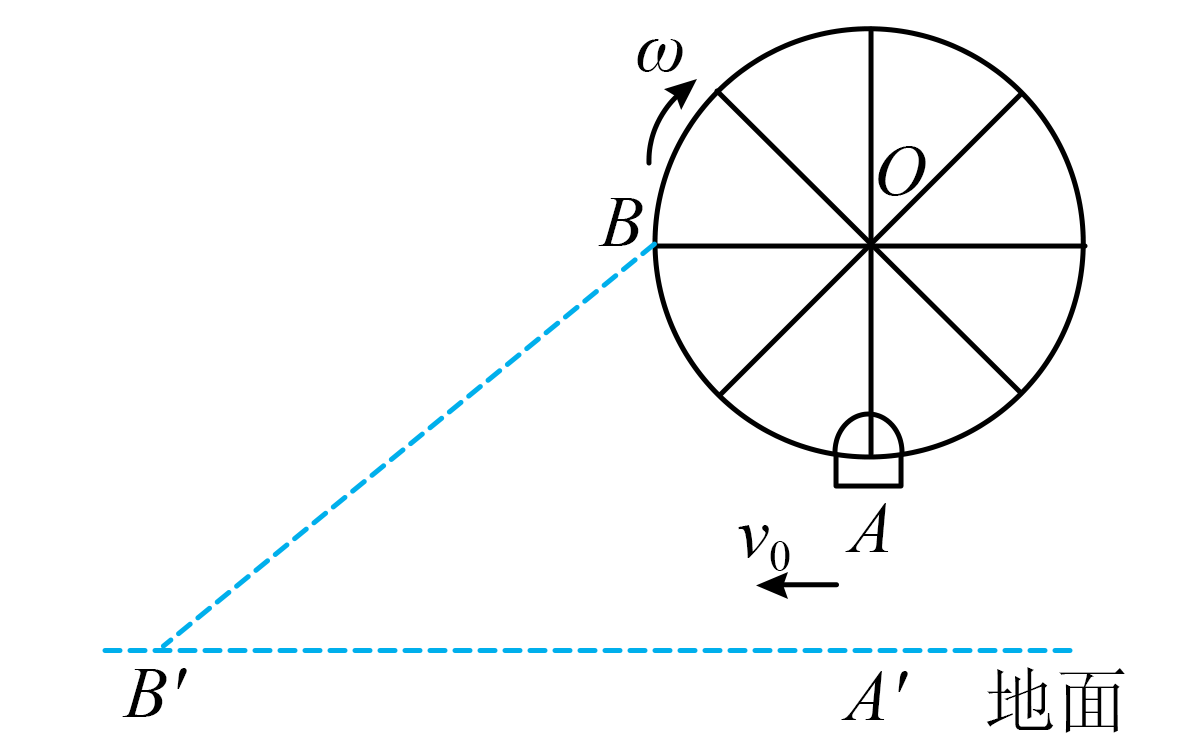
①小明在$A'$点时相对地面的速度$v_{0}$大小为                 $\;\rm m/s$（结果保留$3$位有效数字）。

②质量为$m$的轿厢从$A$点运动到$B$点，其动量的变化量大小的表达式$\Delta p=$                 ，轿厢受到的重力的冲量大小$I_{G}=$                 ，方向为                 （均用题中给出的物理量符号表示）。重力加速度为$g$。

③小明在$B'$点相对地面的速度$v_{1}$大小                 。

摩天轮线速度大小$v_{01}= \dfrac{2\pi R}{T}=\dfrac{2\pi \times 60.0\;\rm{m}}{{960\;\rm s}}= 0.40\;\rm{m/s}$

$A$点的线速度方向水平向左，且此时小明相对此轿厢的速度大小$v=3.50{\;\rm m/s}=v_{0} − v_{01}$

联立解得$v_{0}=3.90\;\rm m/s$

轿厢从$A$点运动到$B$点，速度方向转过$90^\circ $，由矢量三角形法则，其动量的变化量大小表达式$\Delta p=\sqrt{(mv)^{2}+(mv)^{2}}=\sqrt{2}mv_{1}=\dfrac{2\sqrt{2}\pi mR}{T}$

轿厢受到的重力的冲量大小$I_{{G}}=mgt=mg\dfrac{T}{4}$

方向竖直向下；

题意知轿厢运动到摩天轮上与$O$点在同一水平高度的$B$点时小明运动到$B'$点，小明相对此轿厢的速度方向恰好沿$BB'$连线且$B$指向$B'$。根据几何关系有$\dfrac{\dfrac{v_{0}+v_{1}}{2} \times \dfrac{T}{4}-R}{v_{1}}=\dfrac{H}{v_{01}}$

联立解得$v_{1} ≈ 1.24\;\rm m/s$。