如图甲所示，两水平金属板间距为$d$，板间电场强度的变化规律如图乙所示。$t=0$时刻，质量为$m$的带电微粒以初速度$v_{0}$沿中线射入两板间，$0\sim\dfrac{T}{3}$时间内微粒匀速运动，$T$时刻微粒恰好经金属板边缘飞出。微粒运动过程中未与金属板接触。重力加速度的大小为$g$。关于微粒在$0 ∼ T$时间内运动的描述，正确的是$(\qquad)$

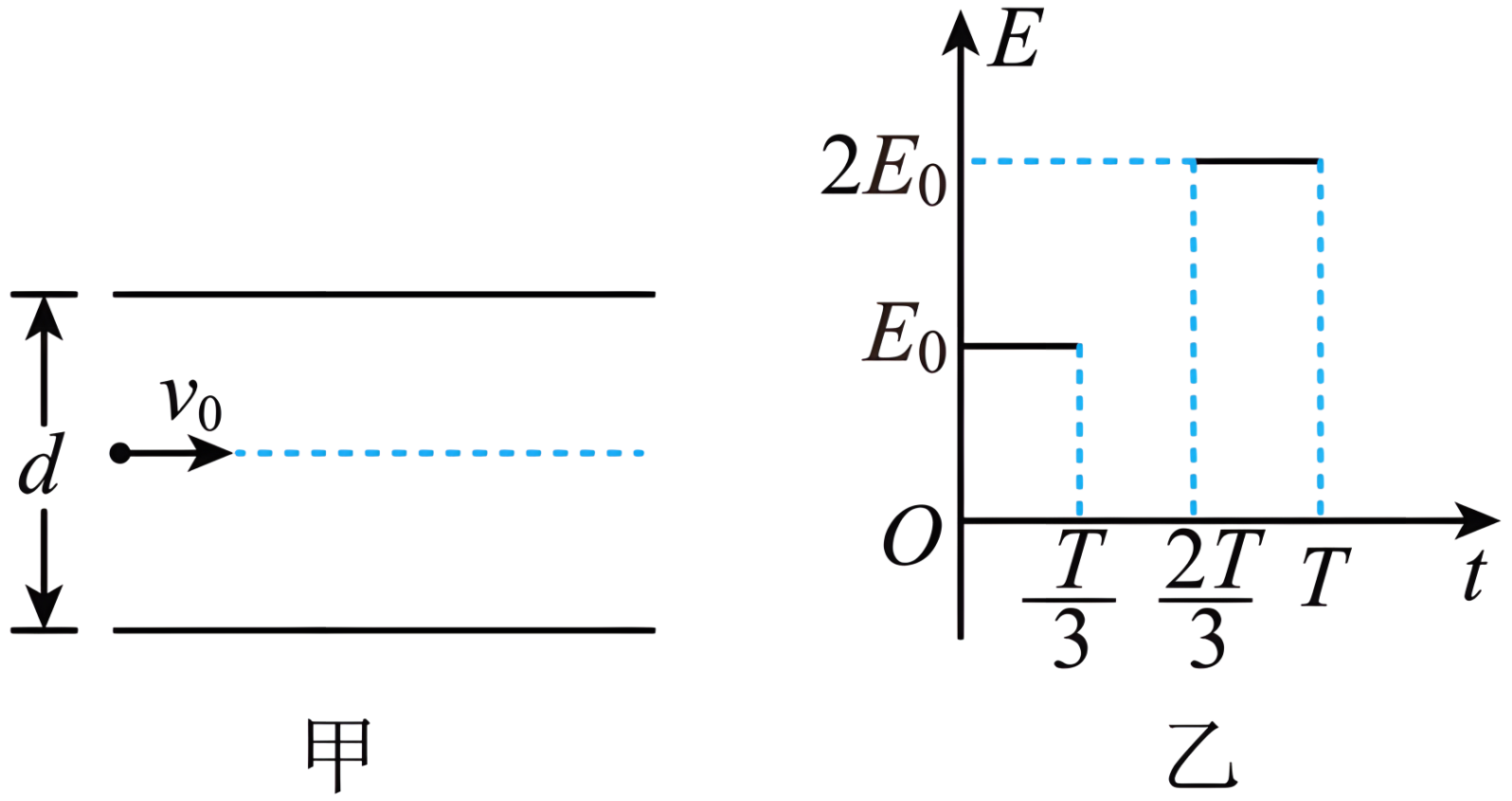
末速度大小为$\\sqrt{2}v_{0}$

重力的冲量为零

克服电场力做功$\\dfrac{1}{2}mgd$

重力势能增加了$\\dfrac{1}{2}mgd$

$\rm A$．$0\sim\dfrac{T}{3}$时间内微粒匀速运动，则有$mg=qE_{0}$

在$\dfrac{T}{3}\sim\dfrac{2T}{3}$内，微粒做平抛运动；在$\dfrac{2T}{3}\sim T$内，微粒受到的合力方向向上，大小为$F=2qE_{0}-mg=mg$

在竖直方向上根据对称性可知，$T$时刻竖直方向上的分速度为零，则微粒末速度大小为$v_{0}$，故$\rm A$错误；

$\rm B$．根据$I_{G}=mgt$

可知重力的冲量不为零，故$\rm B$错误；

$\rm D$．微粒沿金属板边缘飞出，竖直方向上向下运动的位移为$\dfrac{d}{2}$，则重力势能减少了$\dfrac{1}{2}mgd$，故$\rm D$错误。

$\rm C$．在$\dfrac{2T}{3}\sim T$时间内，合力为$F=2qE_{0}-mg=mg$

在竖直方向上根据对称性可知，此过程微粒竖直方向上向下运动的位移为$\dfrac{d}{4}$，所以克服电场力做功为$W=2qE_{0} \cdot \dfrac{d}{4}=\dfrac{1}{2}mgd$

故$\rm C$正确。

故选：$\rm C$。