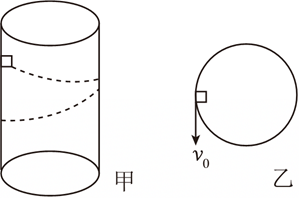
如图甲所示，半径为$R$、内壁光滑的圆柱形圆筒竖直固定，在距底面高$h$处将一小滑块以初速度$v_0$沿水平切线方向射入圆筒（俯视图如图乙所示），小滑块将沿圆筒内壁旋转滑下。在滑块下滑到底端的过程中，下列说法正确的是$(\quad\ \ \ \ )$

筒壁对滑块的弹力逐渐增大

仅增大$v_0$，滑块运动的时间减少

仅增大$h$，滑块旋转的圈数不变

仅减小$R$，滑块运动的路程不变

$\rm A$、滑块在竖直方向做自由落体运动，在水平面内做匀速圆周运动，圆筒壁对小滑块的弹力提供向心力，小滑块圆周运动的向心力大小不变，圆筒壁对小滑块的弹力大小不变，故$\rm A$错误；

$\rm B$、滑块在竖直方向做自由落体运动，竖直分位移$h=\dfrac{1}{2}g{{t}^{2}}$，运动时间$t=\sqrt{\dfrac{2h}{g}}$，仅增大$v_{0}$，滑块的运动时间不变，故$\rm B$错误；

$\rm C$、滑块做匀速圆周运动的周期$T=\dfrac{2\pi R}{{{v}_{0}}}$，滑块旋转的圈数$n=\dfrac{t}{T}$，仅增大$h$，$T$不变而$t$增加，旋转圈数增加，故$\rm C$错误；

$\rm D$、滑块的路程$s=n\cdot 2\pi R=\dfrac{t}{T}\cdot 2\pi R={{v}_{0}}\sqrt{\dfrac{2h}{g}}$，仅减小$R$，滑块运动的路程不变，故$\rm D$正确。

故选：$\rm D$。