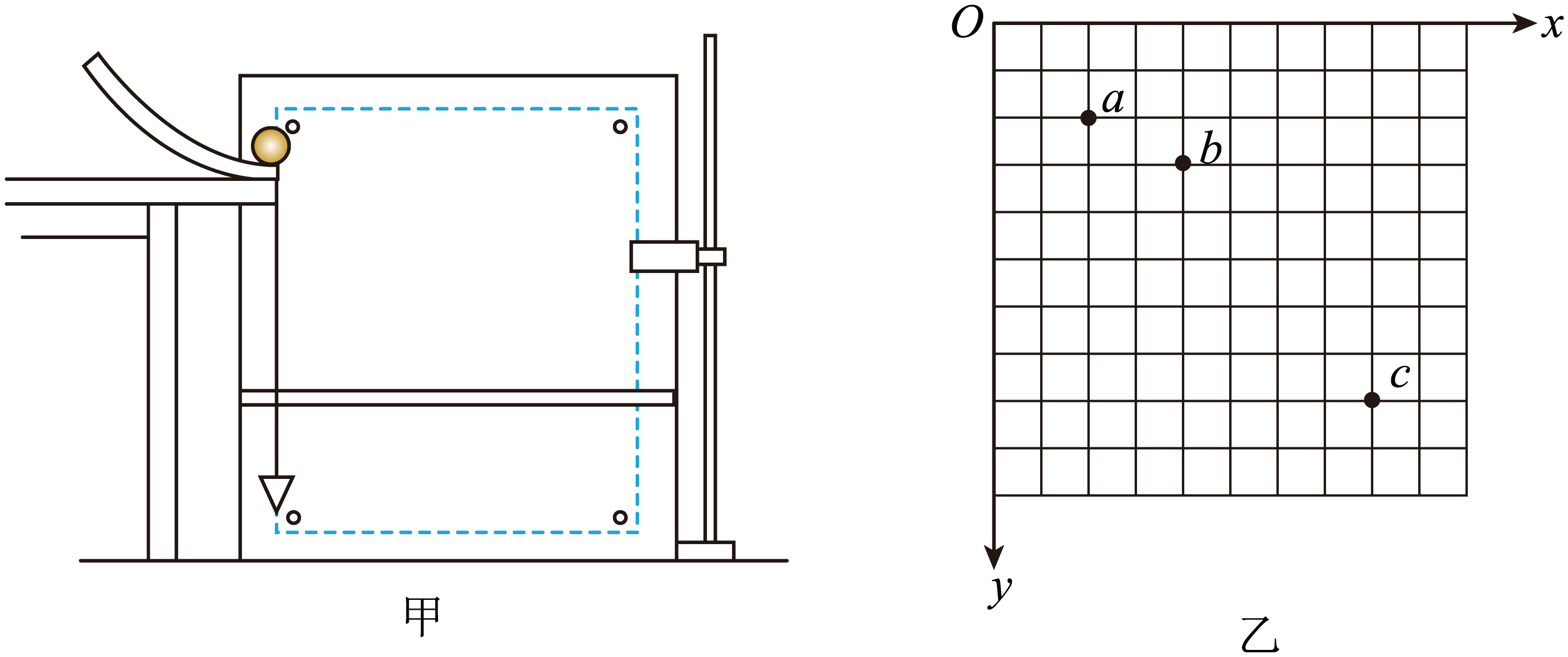
他们利用如图甲所示的实验装置，用“描迹法”测量小球做平抛运动的初速度大小。关于该实验，下列说法正确的是$(\quad\ \ \ \ )$

斜槽轨道末端应保持水平

应想办法尽量减小小球与轨道之间的摩擦

每次应将小球从斜槽轨道上同一位置由静止释放

实验时，必须控制挡板高度等间距下降

A．为保证小球初速度水平，斜槽轨道末端应保持水平，故A正确；

B．小球与轨道之间的摩擦对实验结果无影响，故B错误；

C．为保证小球初速度相等，每次应将小球从斜槽轨道上同一位置由静止释放，故C正确；

D．挡板高度无需等间距下降，故D错误；

故选AC。

该小组正确实验后，在方格纸上记录了小球在不同时刻的位置如图乙中$a$、$b$、$c$所示，建立如图所示的平面直角坐标系，$y$轴沿竖直方向，方格纸每一小格的边长为$L$，$a$、$b$、$c$三点的坐标分别为$a$（$2$$L$，$2$$L$）、$b$（$4$$L$，$3$$L$）、$c$（$8$$L$，$8$$L$）。小球从$a$点到$b$点所用时间为${{t}_{1}}$，$b$点到$c$点所用时间为${{t}_{2}}$，则$\dfrac{{{t}_{2}}}{{{t}_{1}}}=$                    ；在小球轨迹上取一个点$d$（图中未画出），使得小球从$b$点到$d$点和从$d$点到$c$点的运动时间相等，则$d$点的纵坐标为                  。

由图可知$\dfrac{{{x}_{ab}}}{{{x}_{bc}}}=\dfrac{1}{2}$，根据水平方向做匀速直线运动可知$x={{v}_{0}}t$，则$\dfrac{{{t}_{2}}}{{{t}_{1}}}=2$，根据水平方向做匀速直线运动可知相邻两点的水平距离相等，竖直方向满足$\Delta y={{y}_{cd}}-{{y}_{bd}}={{y}_{bd}}-{{y}_{ab}}$，设$d$点的纵坐标为${{y}_{d}}$，则$8L-{{y}_{d}}-({{y}_{d}}-3L)=({{y}_{d}}-3L)-L$，解得${{y}_{d}}=5L$。

若$L=2.45\ \text{cm}$ ，当地重力加速度的大小为$\rm 9.8\ m/s^{2}$，则小球做平抛运动的初速度大小为${{v}_{0}}=$                  $\rm m/s$。（计算结果保留$2$位有效数字）

竖直方向有$\Delta y=g{{T}^{2}}$，水平方向有${{v}_{0}}=\dfrac{2L}{T}$，解得$v_{0}=0.98\ \text{m/s}$。

该实验小组又设计一个新的方案，如图丙所示。$O$点处有一点光源，$O$点正前方$d$处竖直放置一块毛玻璃，将小球从$O$点垂直毛玻璃水平抛出，在毛玻璃后方观察到小球在毛玻璃上的投影点$P$，利用频闪相机记录小球在毛玻璃上的投影点$P$的位置。可得到$P$沿毛玻璃下降的高度$h$随小球运动时间$t$变化的关系如图丁所示，若该图像斜率为$k$，重力加速度为$g$，则小球做平抛运动的初速度大小为                  。（用$k$、$d$和$g$表示）

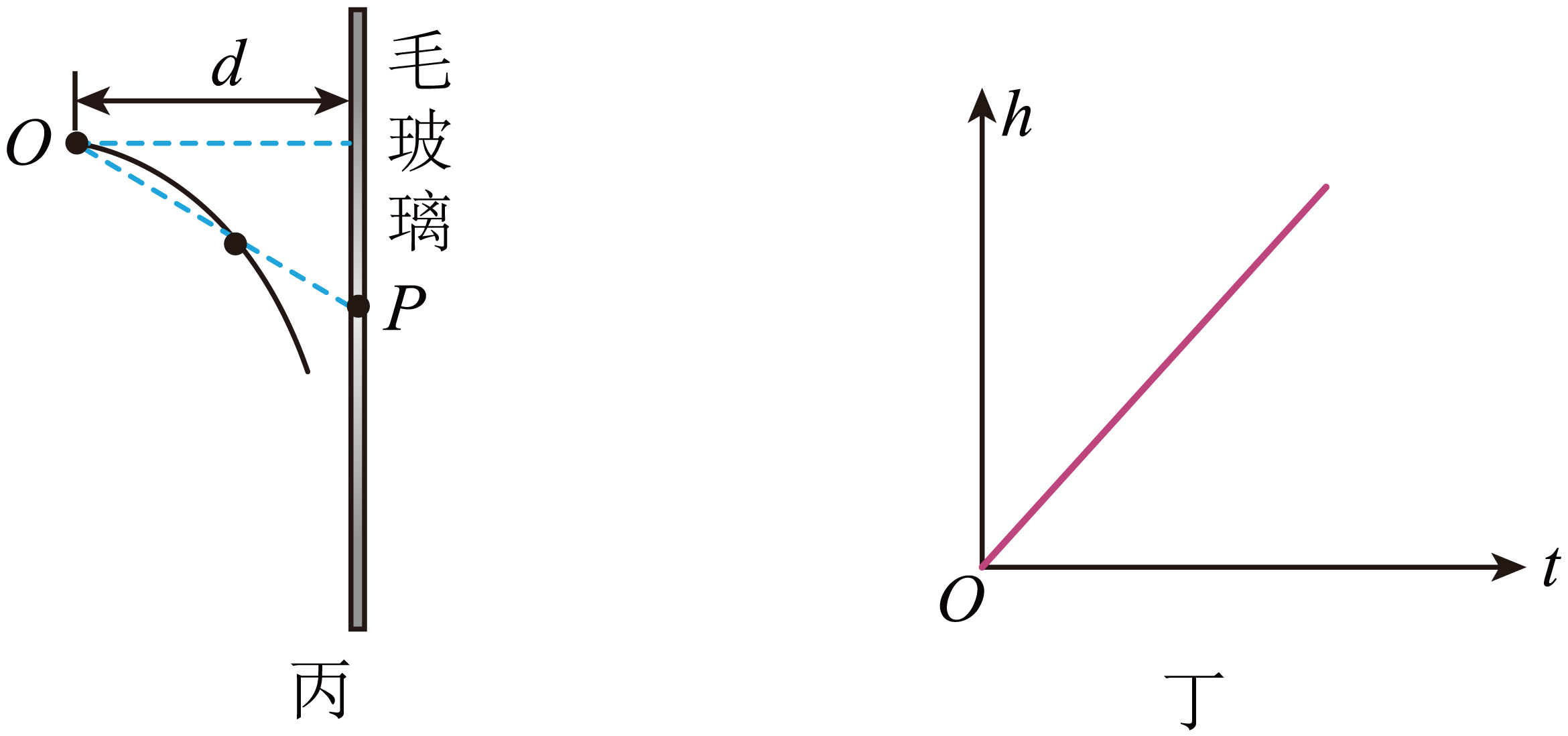
根据平抛运动规律有$d={{v}_{0}}t$，$h=\dfrac{1}{2}g{{t}^{2}}$，解得$h=\dfrac{gd}{2{{v}_{0}}}t$，则斜率为$k=\dfrac{gd}{2{{v}_{0}}}$，解得${{v}_{0}}=\dfrac{gd}{2k}$。