已知图$1$中$A$、$B$齿轮啮合且齿轮之间不打滑，$B$、$C$齿轮同轴，若$A$、$B$、$C$三齿轮半径的大小关系为$r_{A}=2r_{B}$、$r_{B}=3r_{C}$，则$(\qquad)$

齿轮$A$、$B$边缘的角速度之比为$2:1$

齿轮$B、C$边缘的角速度之比为$1:3$

齿轮$B$、$C$边缘的向心加速度大小之比为$1:2$

齿轮$A$、$C$边缘的向心加速度大小之比为$3:2$

$\rm A$．由$A$、$B$齿轮啮合且齿轮之间不打滑，可知$v_{A}=v_{B}$，由角速度与线速度之间的关系$v_{A}=\omega_{A} ⋅ r_{A}$，$v_{B}=\omega_{B} ⋅ r_{B}$，结合$A$、$B$之间半径的关系，可得$\omega_{A}:\omega_{B}=r_{B}:r_{A}=1:2$，$\rm A$选项错误；

$\rm B$．由$B$、$C$齿轮同轴，可知两者角速度相等，齿轮$B$、$C$边缘的角速度之比为$1:1$，$\rm B$选项错误；

$\rm C$．由向心加速度和角速度关系$a_{n}=\omega^{2}r$，可得$a_{nB}:a_{nC}=r_{B}:r_{C}=3:1$，$\rm C$选项错误；

$\rm D$．由向心加速度和线速度关系$a_{n}=\dfrac{v}{r}^{2}$，可得$a_{nA}:a_{nB}=r_{B}:r_{A}=1:2$，故而$A$、$C$边缘的向心加速度大小之比$a_{nA}:a_{nC}=3:2$，$\rm D$选项正确。

故选： $\rm D$。

小葛同学尝试只用一把卷尺，测量图中水泵的最大出水量（即出水口单位时间内流出的水的最大体积）$V_{0}$。步骤如下：

①关闭水阀，用卷尺测出出水口的内直径为$D$；

②测出出水口离地高度为$h$，打开水阀门且将其调到出水量最大，记下喷出的水落地的平均位置，关上阀门，测量出平均位置到出水口的水平距离为$L$，已知重力加速度为$g$，忽略空气阻力，则出水口的水速大小$v=$                 （用已知物理量的字母表示）；

③请推导$V_{0}$表达式：$V_{0}=$                 （用已知物理量的字母表示）。

①。由分析可知，水流自出水口出去之后做平抛运动，水平匀速直线运动关系式$L=vt$

竖直方向自由落体运动关系式$h=\dfrac{1}{2}gt^{2}$

联立可得$v=L\sqrt{\dfrac{g}{2h}}$

②。由流体体积公式$V_{0}=Sv$

出水口截面积为$S=\pi\left( \dfrac{D}{2} \right)^{2}=\dfrac{\pi D^{2}}{4}$

联立可得$V_{0}=\dfrac{\pi D^{2}L}{4}\sqrt{\dfrac{g}{2h}}$

有时需要扩大灌溉面积，可以在出水管末端加装一段细管，如图所示。保持细管水平且高度不变，粗管内单位时间的进水量不变，则加装细管后$(\qquad)$

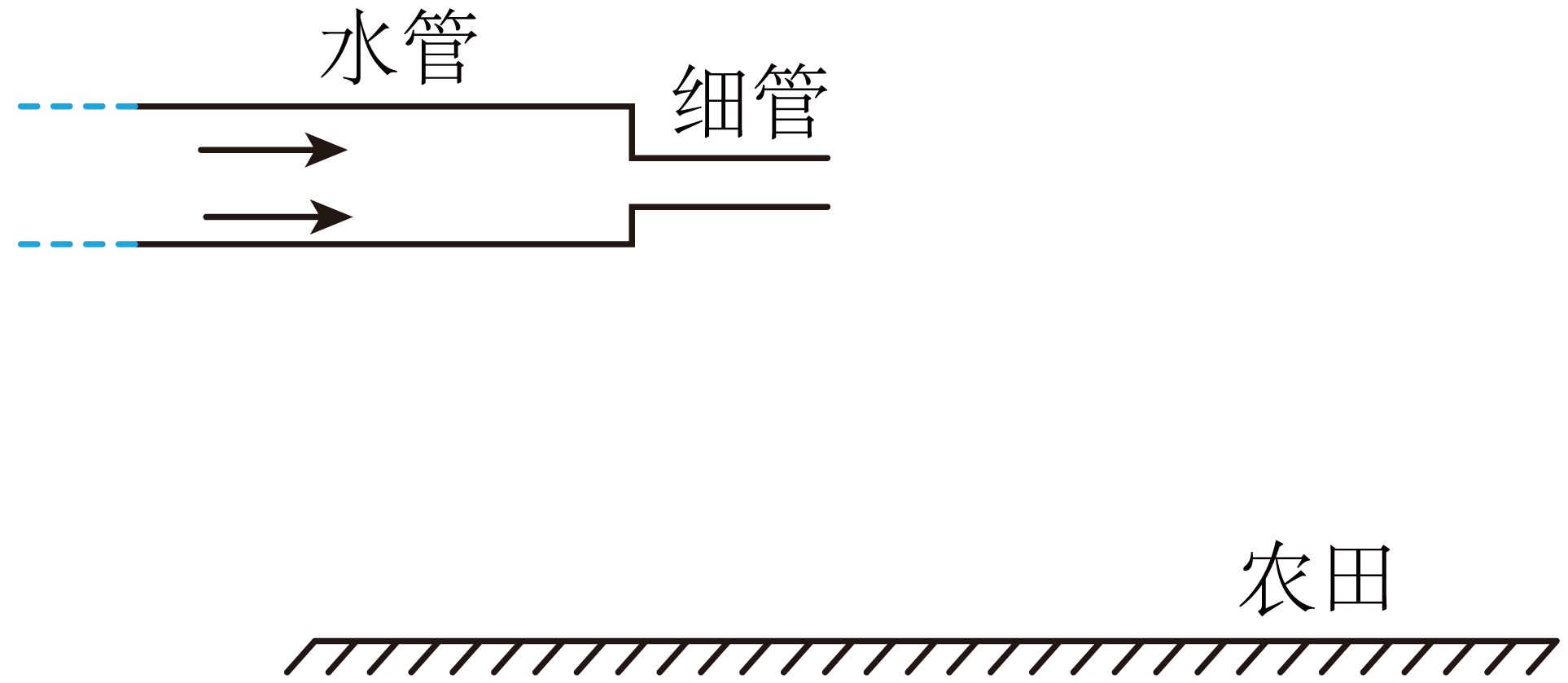
喷出的水的出口速度不变

喷出的水的水平射程将变大

单位时间内的出水量将显著增加

喷出的水在空中运动的时间将变长

$\rm AB$．由流体体积公式$V_{0}=Sv$，由图可知出水口直径变小，横截面积变小，粗管内单位时间的进水量不变，则喷出的水的出口速度变大，进而水平射程将变大，$\rm A$选项错误，$\rm B$选项正确；

$\rm C$．粗管内单位时间的进水量不变，单位时间内的出水量也不变，$\rm C$选项错误；

$\rm D$．平抛运动的运动时间只与落地高度有关，保持细管水平且高度不变，则喷出的水在空中运动的时间不变，$\rm D$选项错误。

故选： $\rm B$。

随着科技进步，可利用卫星来感知灌溉信息，智慧助农。一极地卫星在距地面高度为$d$、且通过地球南北两极正上方的圆轨道上运行，监测的农田南北长为$L$，地球的半径为$R$，地球表面重力加速度为$g$，忽略地球自转，该卫星通过农田正上方的时间为$(\qquad)$

$\\dfrac{(R+d)L}{R^{2}}\\sqrt{\\dfrac{R}{g}}$

$\\dfrac{RL}{(R+d)^{2}}\\sqrt{\\dfrac{R+d}{g}}$

$\\dfrac{(R+d)L}{R^{2}}\\sqrt{\\dfrac{R+d}{g}}$

$\\dfrac{(R+d)L}{R^{2}}\\sqrt{\\dfrac{g}{R+d}}$

卫星绕地球做匀速圆周运动，万有引力提供向心力，由牛顿第二定律得$G\dfrac{Mm}{(R+d)^{2}}=m\omega^{2}(R+ d)$

地面上物体受到的重力等于万有引力，即$G\dfrac{Mm'}{R^{2}}=m'g$

设卫星经过农田所用时间为$t$，则农田所对应圆心角$\theta=\dfrac{L}{R}=\omega t$

解得$t=\dfrac{L}{R\omega}=\dfrac{(R+d)L}{R^{2}}\sqrt{\dfrac{R+d}{g}}$

故选：$\rm C$。