如图，一束太阳光自矩形玻璃砖上表面$O$点射入玻璃砖内，光经玻璃砖折射后照射在玻璃砖下表面$ab$区域，再从玻璃砖下表面射出（图中未画出）。已知频率越大的光在玻璃中的传播速度越小。

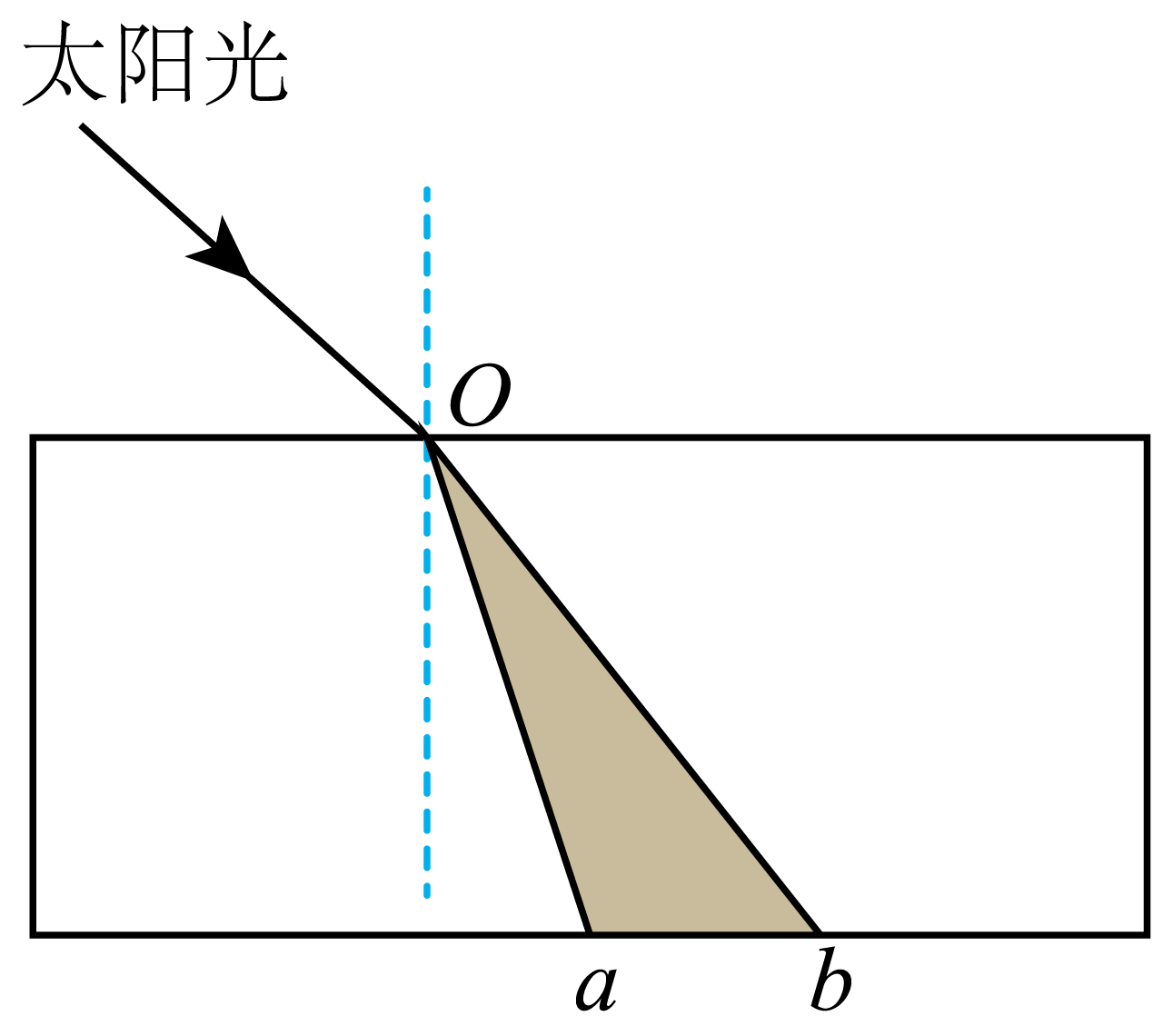
①从玻璃砖下表面$a$点射出的光               ；

$\rm A$．为红光      $\rm B$．为紫光      $\rm C$．与$b$点射出的光平行      $\rm D$．与入射的太阳光平行

②在太阳光入射到$O$点的传播路径上放一块偏振片，从玻璃砖下表面射出的光的亮度               ；

$\rm A$．变暗      $\rm B$．变亮      $\rm C$．不变

$\rm AB$．太阳光为复色光，在玻璃中，紫光频率比红光大 ，由 “频率越大的光在玻璃中的传播速度越小”，根据$n= \dfrac{c}{v}$可知紫光在玻璃中的折射率比红光大。根据折射定律，在入射角相同情况下，紫光折射角小，更靠近法线，所以从$a$点射出的不是红光，是紫光，故$\rm A$错误，$\rm B$正确；

$\rm CD$．根据光的折射规律，光线通过平行玻璃砖时， 经过两次折射，出射光线与入射光线平行，所以从玻璃砖下表面射出的光与入射的太阳光平行，故$\rm C$错误，$\rm D$正确；

故选：$\rm BD$；

偏振片可以只让沿某一方向振动的光通过 ，太阳光为自然光，向各个方向振动的光的强度都相同。在太阳光入射路径上放偏振片，会过滤掉部分振动方向的光，通过偏振片后的光强度减弱，再经过玻璃砖折射后射出的光亮度也会变暗；

故选：$\rm A$；

通过对宇宙的观测和研究，我们发现$(\qquad)$

光在真空中一定沿直线传播

在不同的惯性参考系中，物理规律的形式不同

在密闭的太空飞行器中不能判断飞行器是否加速

因宇宙膨胀，我们观测到遥远星系发出的光的频率减小

$\rm A$．光在真空中只有在均匀介质中才沿直线传播，当存在引力场等情况时，光线会发生弯曲 ，比如在强引力场附近，光会因时空弯曲而不沿直线传播，故$\rm A$错误；

$\rm B$．根据狭义相对论的相对性原理，在不同的惯性参考系中，物理规律的形式是相同的，这是狭义相对论的基本假设之一，故$\rm B$错误；

$\rm C$．在密闭的太空飞行器中，可以通过一些实验，比如利用加速度计等仪器来判断飞行器是否加速，故$\rm C$错误；

$\rm D$．由于宇宙膨胀，遥远星系远离我们，根据多普勒效应，会出现红移现象，即我们观测到遥远星系发出的光的频率减小，波长变长，故$\rm D$正确；

故选：$\rm D$；

如图，当月球恰好完全挡住太阳射向地球的光，地球上的观察者就观察到日全食现象。已知太阳直径约为月球直径的$400$倍，光从太阳到地球用时约为$499$秒。则光从月球到地球用时约为                 $\;\rm s$（结果保留三位有效数字）。若太阳的质量约为地球质量的$n$倍，则地球绕太阳公转速度约为月球绕地球公转速度的                 倍；

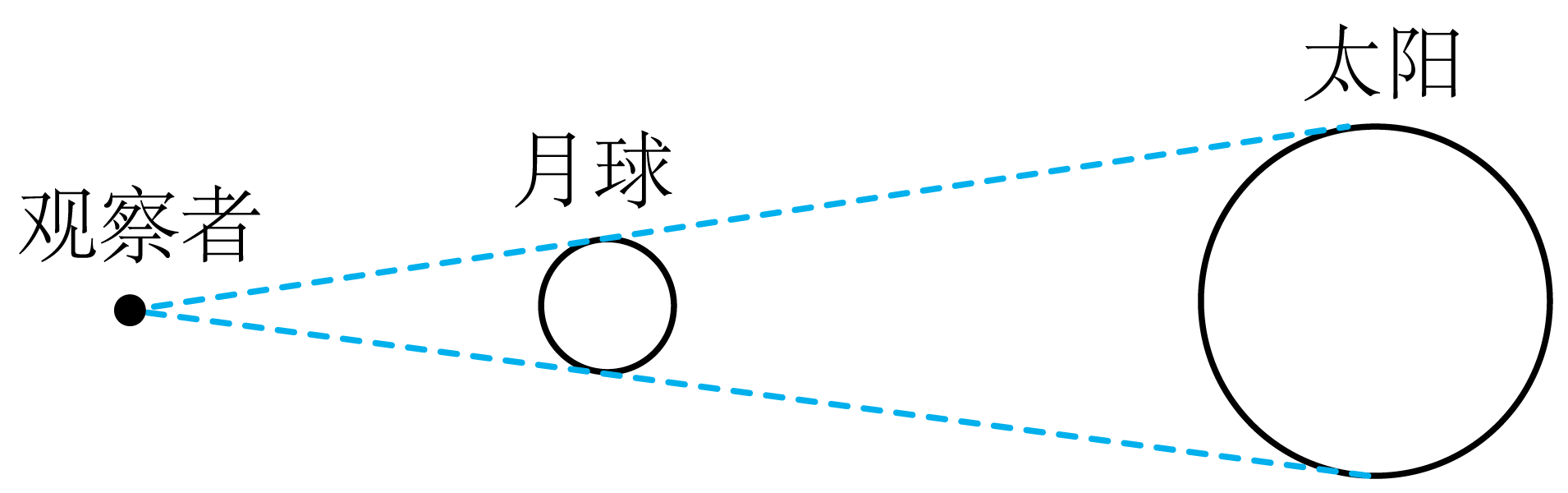
根据相似三角形可知，太阳直径、月球直径的比值等于太阳、地球距离与月球、地球距离，光在真空速度相同，故有$\dfrac{t_{太地}}{t_{月地}}=\dfrac{400}{1}= \dfrac{499}{t_{月地}}$，解得$t_{月地}=1.25\;\rm s$

根据$\dfrac{GMm}{r^{2}}=m\dfrac{v^{2}}{r}$，解得$v=\sqrt{\dfrac{GM}{r}}$，因为$\dfrac{r_{太地}}{r_{月地}}=\dfrac{400}{1}$，$M_{太}=nM_{地}$，联立解得$\dfrac{v_{太地}}{v_{月地}}=\dfrac{\sqrt{n}}{20}$；

科学家发现某恒星发出某一固定频率的光。如图所示，将这种频率的光通过窗口$C$入射到抽成真空的容器内的金属板$K$上。已知电子电荷量为$e$，普朗克常量为$h$，金属板材料的截止频率为$v_{0}$。

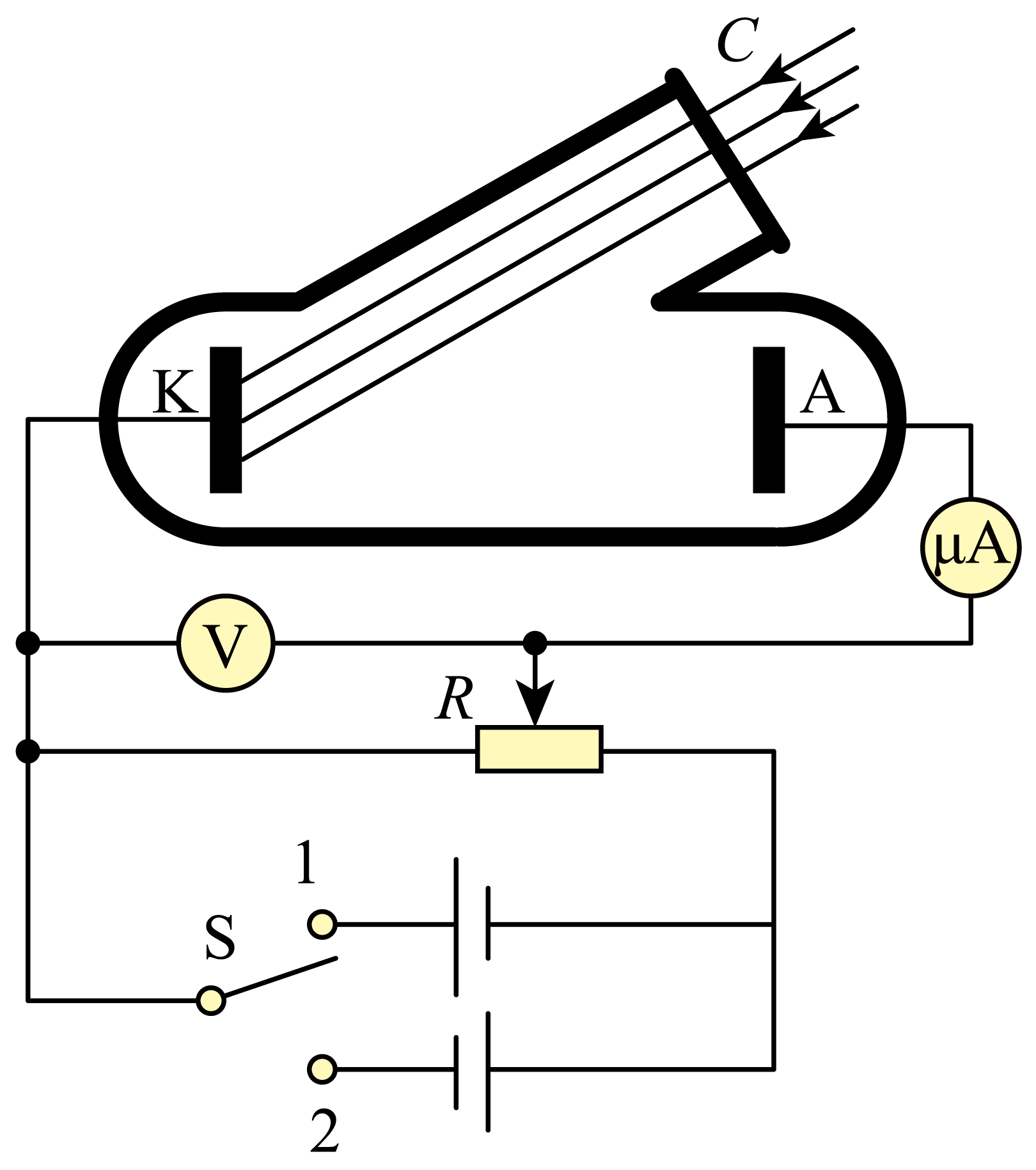
①为测量饱和光电流

$i.$将单刀双掷开关$\rm S$置于             ；

$\rm A$．位置$1$      $\rm B$．位置$2$

$ii.$移动滑动变阻器的滑片，当光电流达到最大值时电流表的示数为$I_{m}$，可估算单位时间内到达$A$板的电子数约为                 ；

②将单刀双掷开关$\rm S$置于另一位置来测量光的频率。

$i.$移动滑动变阻器的滑片，使                 ，此时另一个电表的示数为$X$；

$ii.$光的频率表达式为                 ；

要测量饱和光电流，需在光电管两端加正向电压，使光电子能顺利从$K$板到达$A$板 。当单刀双掷开关$\rm S$置于位置$2$ 时，电源给光电管加正向电压，能使光电流达到饱和；

故选：$\rm B$；

单位时间内到达$A$板的电子数所带电荷量即为电流值，即有$I_{\rm m}=Ne$

单位时间内到达$A$板的电子数约为$N=\dfrac{I_{\rm {m}}}{e}$

将单刀双掷开关$\rm S$置于位置$1$时，光电管加反向电压。当移动滑动变阻器滑片，使反向电压增大到某一值时，具有最大初动能的光电子也恰好不能到达$A$板，此时光电流为零（即电流表示数为$0$），这个反向电压就是遏止电压 。

根据光电效应方程$E_{\rm km}=h\nu − W_{0}$

因为$E_{\rm km}=eU_{c}=eX$，$W_{0}=hv_{c}$

联立解得光的频率表达式$v=\dfrac{eX}{h}+v_{c}$；

宇宙射线携带的$a$、$b$两种粒子穿过云室，在磁感应强度大小为$B$的匀强磁场作用下得到如图的圆形径迹照片，磁场方向与粒子运动轨迹的平面垂直。经观测可知，

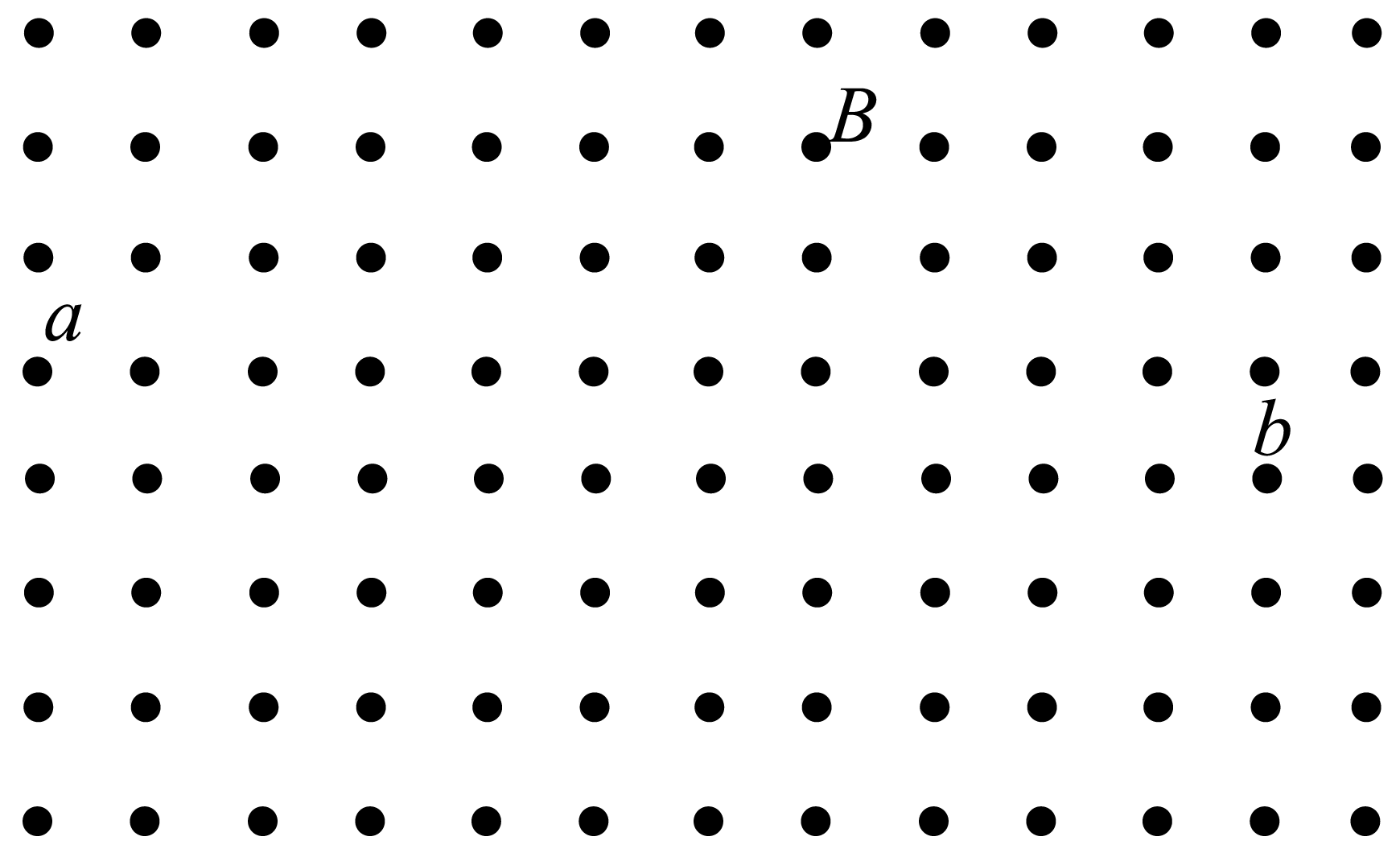
①$a$粒子在磁场中逆时针做圆周运动，$b$粒子在磁场中顺时针做圆周运动。             

$\rm A$．$a$、$b$粒子都带正电          $\rm B$．$a$、$b$粒子都带负电

$\rm C$．$a$粒子带正电，$b$粒子带负电      $\rm D$．$a$粒子带负电，$b$粒子带正电

②$a$、$b$两种粒子做圆周运动的半径关系为：$R_{a} \gt R_{b}$，周期关系为：$T_{a} \lt T_{b}$，分析说明$a$、$b$粒子的比荷关系为：$\dfrac{q_{a}}{m_{a}} \gt \dfrac{q_{b}}{m_{b}}$                 。

根据题意，$a$粒子在磁场中逆时针做圆周运动，左手定则可知$a$粒子带负电；$b$粒子在磁场中顺时针做圆周运动，左手定则可知$b$粒子带正电，

故选：$\rm D$。

带电粒子在磁场中仅受磁场力而做匀速圆周运动，圆周运动周期$T=\dfrac{2\pi m}{qB}$

题意知$T_{a} \lt T_{b}$，则有$\dfrac{2\pi m_{a}}{q_{a}B} \lt \dfrac{2\pi m_{b}}{q_{b}B}$

整理得$\dfrac{q_{a}}{m_{a}} \gt \dfrac{q_{b}}{m_{b}}$。