如图所示为$F1$赛车的“上”字形赛道示意图，赛车$(\quad\ \ \ \ )$。

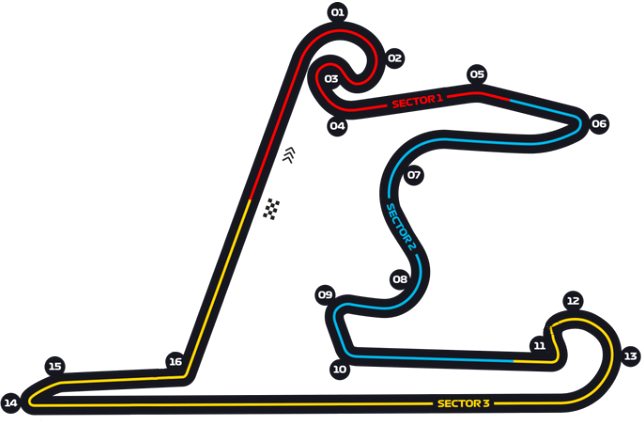
一定可看作质点

拐弯时速度不变

运动一周位移为零

运动一周平均速度为零

$\rm A$．当物体的大小和形状相对于研究的问题而言可以忽略不计，则可以作为质点，若要研究赛车转弯时车轮的转动情况，则此时赛车不能作为作为质点，故$\rm A$错误；

$\rm B$．拐弯时，赛车做曲线运动，速度方向时刻在改变，故速度变化，故$\rm B$错误；

$\rm CD$．赛车运动一周，初末位置一样，则位移为零，平均速度$\overline{v}=\dfrac{x}{t}$也为零，故$\rm CD$正确。

故选：$\rm CD$。

赛车采用的是后轮驱动系统，起动时后轮和前轮对地面的摩擦力方向分别为$(\quad\ \ \ \ )$。

向前、向前

向后、向后

向前、向后

向后、向前

赛车采用后轮驱动系统，则起动时后轮有相对于地面向后的运动趋势，则后轮受到地面向前的摩擦力，根据牛顿第三定律可知起动时后轮对地面的摩擦力方向向后；起动时前轮所受摩擦力向后，根据牛顿第三定律可知起动时前轮对地面的摩擦力方向向前。

故选：$\rm D$。

某弯道倾角为$\theta$，赛车转弯半径为$r$，若赛车无侧向滑动趋势，则其速度大小$v$为                 。（重力加速度大小为$g$）

由牛顿第二定律$mg\tan\theta= m\dfrac{v^{2}}{r}$

可得其速度大小为$v=\sqrt{gr\tan\theta}$

直线加速赛采用全长$1500\;\rm m$的直线跑道。在$\dfrac{1}{4}$英里的直线加速比赛中，某辆赛车从静止起动，跑完$\dfrac{1}{4}$英里（约$402\;\rm m$）所用的时间仅为$3.8\;\rm s$，尾速达到$523\;\rm km/h$。

①有同学认为该赛车的运动为匀加速直线运动，请通过计算论证该观点是否正确                 。

②赛车跑完$\dfrac{1}{4}$英里后立即制动。若用传统刹车系统，平均制动力约为车重的$0.6$倍。通过计算判断采用传统刹车系统是否合理。（重力加速度大小$g$取$10\;\rm m/s^{2}$）                 

①设赛车做匀加速直线运动，由运动学公式$s=\dfrac{1}{2}at^{2}$

可得$a=\dfrac{2s}{t^{2}}=\dfrac{2 \times 402}{{3.8}^{2}}\;\rm \text{m/s}^{2}=\dfrac{20100}{361}\ \text{m/s}^{2}$

末速度为$v=at=\dfrac{20100}{361} \times 3.8\;\rm \text{m/s} \approx 212\;\rm \text{m/s} \approx 763\;\rm \text{km/h}$大于尾速$523\;\rm km/h$。

故说明赛车的运动不是匀加速直线运动。

②刹车时由牛顿第二定律$f=ma$可得赛车刹车时的加速度大小为$a=\dfrac{f}{m}=\dfrac{0.6mg}{m}=0.6g$

由运动学公式$v^{2}=2ax$

其中$v=\dfrac{523}{3.6}\text{m/s}$，解得$x\approx 1759\;\rm m$

而剩余赛程为$x'=1500\;\rm m-402\;\rm m=1098\;\rm m$

由于$1759\;\rm m\gt 1098\;\rm m$

所以采用传动刹车系统不合理。

狭义相对论告诉我们，长度收缩也是相对的。一辆赛车在赛道上飞驰，$(\quad\ \ \ \ )$。

看台上的观众认为赛车变短了，赛车手认为赛道变短了

看台上的观众认为赛车变短了，赛车手认为赛道变长了

看台上的观众认为赛车变长了，赛车手认为赛道变短了

看台上的观众认为赛车变长了，赛车手认为赛道变长了

狭义相对论告诉我们，长度收缩也是相对的。一辆赛车在赛道上飞驰，看台上的观众认为赛车变短了，赛车手认为赛道变短了。

故选：$\rm A$。