核心舱和地面间使用无线电波联系，核心舱内宇航员之间使用声波交流。无线电波和声波的特点$(\qquad)$

都不需要介质传播

都属于电磁波

都能传递能量和信息

都能发生干涉和衍射

$\rm AB$．无线电波属于电磁波，不需要介质传播；声波属于机械波，需要介质传播；故$\rm AB$错误；

$\rm CD$．根据波的特性可知，无线电波和声波都能传递能量和信息，都能发生干涉和衍射，故$\rm CD$正确；

故选：$\rm CD$；

航天员乘组随火箭加速上升过程中，处于超重状态。

①他们受到地球的引力逐渐                 （选填“变大”、“不变”或“变小”）；

②在进入核心舱后几乎处于完全失重状态，则他们$(\qquad)$

$\rm A$．受地球引力，无加速度                       $\rm B$．受地球引力，有加速度

$\rm C$．无地球引力，无加速度                      $\rm D$．无地球引力，有加速度

①航天员乘组随火箭加速上升过程中，与地球的距离越来越大，根据$F_{引}=\dfrac{GMm}{r^{2}}$

可知他们受到地球的引力逐渐变小；

②在进入核心舱后几乎处于完全失重状态，则他们受地球引力，加速度等于所在轨道的重力加速度；

故选：$\rm B$；

以地面为参照系，宇航员在地面上的质量为$m_{0}$，在核心舱内的质量为$m$，已知核心舱相对地面的飞行速度为$v$，如果只考虑狭义相对论效应，则$m$和$m_{0}$ 的关系正确的是$(\qquad)$

$m=m_{0}$

$m=m_{0}\\sqrt{1-\\dfrac{c^{2}}{v^{2}}}$

$m=m_{0}\\sqrt{1-\\dfrac{v^{2}}{c^{2}}}$

$m=\\dfrac{m_{0}}{\\sqrt{1-\\dfrac{v^{2}}{c^{2}}}}$

如果只考虑狭义相对论效应，则有$m=\dfrac{m_{0}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}$

故选：$\rm D$；

空间站窗外射进一束阳光，照射到一空心水晶球上。航天员发现水晶球特别明亮，这是光在水晶球内部空气表面发生了全反射现象，如图所示。如果水晶折射的临界角为$C$。

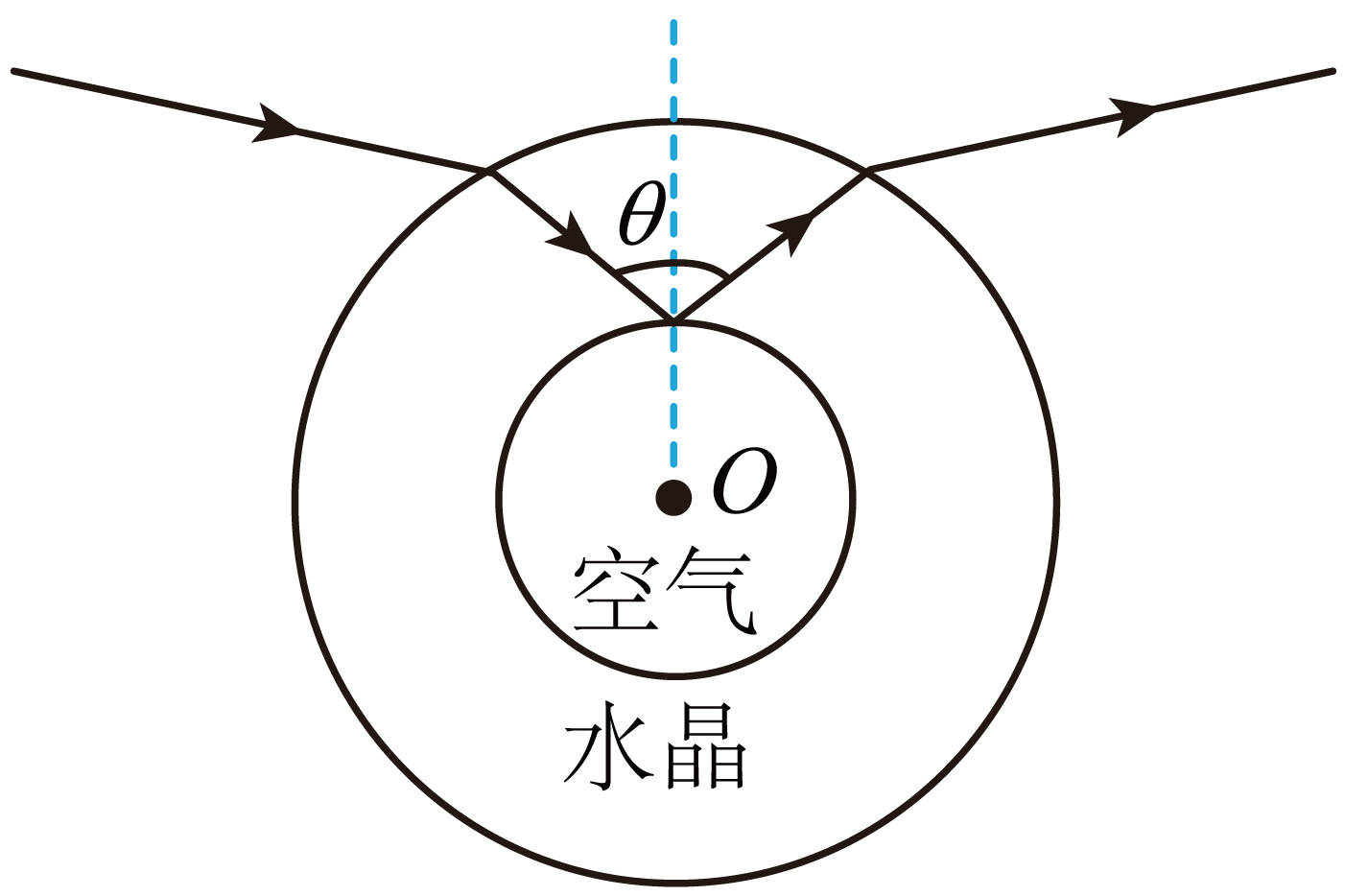
①则水晶的折射率$n=$                 ；

②图中发生全反射的入射光线与反射光线间夹角$\theta$大小一定$(\qquad)$

$\rm A$．等于$C$                      $\rm B$．等于$2C$

$\rm C$．小于$2C$                      $\rm D$．大于等于$2C$

① 水晶折射的临界角为$C$，根据$\sin C=\dfrac{1}{n}$

可知水晶的折射率为$n=\dfrac{1}{\sin C}$

②图中发生全反射的入射光线的入射角一定大于等于$C$，则图中发生全反射的入射光线与反射光线间夹角$\theta$大小一定大于等于$2C$；

故选：$D$；

计算：空间站的运动可以看作为围绕地球的匀速圆周运动。若地球表面重力加速度$g=9.8\;\rm m/s^{2}$，地球半径$R=6400\;\rm km$，空间站轨道离地高度$h=400\;\rm km$。

①求空间站运动的速度$v$；（保留三位有效数字）

②简要说明：空间站的速度为什么小于第一宇宙速度？

①$7.68\\times 10^{3}\\:\\rm m/s$；②见解析

①设地球质量为$M$，物体质量为$m_{1}$，则在地面上有$\dfrac{GMm_{1}}{R^{2}}=m_{1}g$

可得$GM=gR^{2}$

设空间站质量为$m_{2}$，由万有引力提供向心力可得$\dfrac{GMm_{2}}{{(R+h)}^{2}}=m_{2}\dfrac{v^{2}}{R+h}$

联立解得空间站运动的速度为$v=\sqrt{\dfrac{GM}{R+h}}=\sqrt{\dfrac{gR^{2}}{R+h}} \approx 7.68 \times 10^{3}\;\rm{m}/{s}$

②第一宇宙速度等于卫星在地球表面轨道绕地球做匀速圆周运动的线速度，则有$\dfrac{GMm}{R^{2}}=m\dfrac{v_{1}^{2}}{R}$

可得第一宇宙速度为$v_{1}=\sqrt{\dfrac{GM}{R}}$

则有$v=\sqrt{\dfrac{GM}{R+h}} \lt v_{1}=\sqrt{\dfrac{GM}{R}}$。