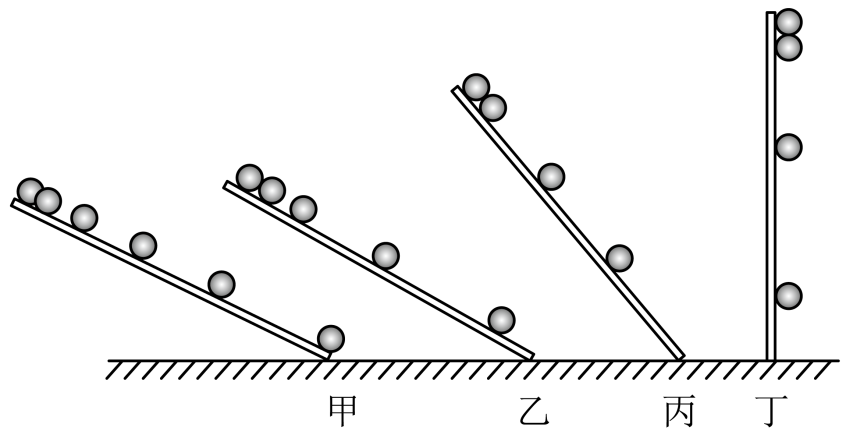
伽利略对自由落体运动的研究，是科学实验和逻辑思维的完美结合，如图所示，可大致表示其实验和思维的过程，对这一过程的分析正确的是$(\qquad)$

伽利略用该实验证明力不是维持物体运动的原因

其中丁图是实验现象，甲图是经过合理外推得到的结论

运用甲图实验，可“冲淡”重力的作用，更方便进行实验测量

运用丁图实验，可“放大”重力的作用，从而使实验现象更明显

$\rm A$．伽利略用该实验研究自由落体运动，而不是为了证明力不是维持物体运动的原因，$\rm A$错误；

$\rm B$．其中甲图是实验现象，丁图是经过合理外推得到的结论，$\rm B$错误；

$\rm C$．伽利略让铜球沿阻力很小的斜面滚下，所用时间容易测量，“冲淡”重力的作用，$\rm C$正确；

$\rm D$．丁图是伽利略根据前面的实验做了合理的外推，不是实验过程，$\rm D$错误；

故选：$\rm C$；

牛顿运动定律成立的参考系称为惯性系，而相对惯性系做                 运动的参考系也是惯性系。伽利略                 原理告诉我们，力学规律在任何惯性系中都具有相同的形式；

相对惯性系做匀速直线运动的参考系，相对惯性系静止，故牛顿定律也成立；

力学规律在任何惯性系中都具有相同的形式，这是伽利略相对性原理；

根据狭义相对论关于时间的相对性，我们把在自身静止的参考系内测得的时间称为                 ，它是最短的；

根据狭义相对论关于时间的相对性，我们把在自身静止的参考系内测得的时间称为固有时，或者本征时间；

伽利略认为最简单的变速运动应是速度均匀变化的，他曾考虑速度对位移均匀变化的可能性。在此基础上，考虑如下问题：在光滑且足够长的水平直杆上放置质量为$m$的小球。小球从$x=0$处开始运动，初速度为$v_{0}$，且受到大小与小球瞬时速度$v$成正比、方向与运动方向相反的阻力，其大小满足$F=kv(k \gt 0)$。设小球在任意时刻速度为$v$、位移为$x$，推导出$v$与$x$之间的函数关系式。并分析小球停止时的位移大小。

$v=- \\dfrac{k}{m}x+v_{0}$，$x_{\\rm\\max}=\\dfrac{mv_{0}}{k}$

由动量定理得$−F\Delta t=mv − mv_{0}$

代入$F=kv(k \gt 0)$得$−kv\Delta t=mv − mv_{0}$，其中$v\Delta t=x$

整理得$v=- \dfrac{k}{m}x+v_{0}$

当小球停止时，$v=0$，代入得$x_{\rm\max}=\dfrac{mv_{0}}{k}$。