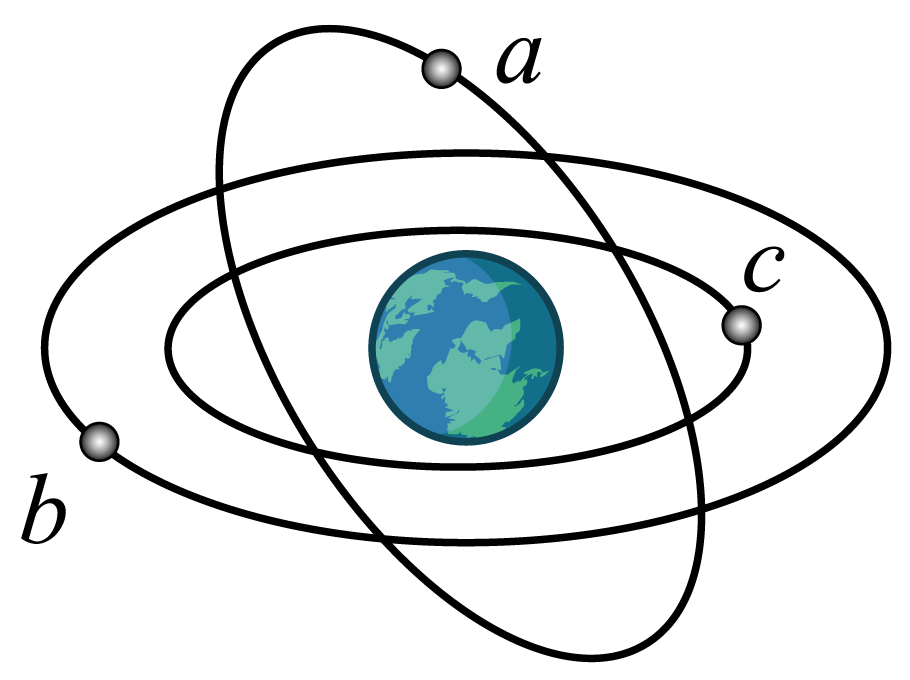
导航卫星的发射速度应$(\quad\ \ \ \ )$。

小于第一宇宙速度

大于第一宇宙速度且小于第二宇宙速度

大于第二宇宙速度

要将导航卫星送入围绕地球的稳定轨道，其发射速度应大于第一宇宙速度，又必须小于第二宇宙速度，否则会逃逸。

故选：$\rm B$。

运载火箭将卫星从地面发射时，假设在舱内放置一个单摆，此时单摆周期$(\quad\ \ \ \ )$在地面时的周期。

小于

大于

等于

火箭发射时，舱内单摆所受的等效重力加速度大于重力加速度$g$，根据单摆周期公式$T= 2\pi\sqrt{\dfrac{L}{g}}$可得单摆的周期小于在地面时的周期。

故选：$\rm A$。

卫星$a$、$b$、$c$的线速度分别为$v_{a}$、$v_{b}$、$v_{c}$，角速度分别为$\omega_{a}$、$\omega_{b}$、$\omega_{c}$，则$(\quad\ \ \ \ )$。

$\\dfrac{v_{a}}{v_{c}}=\\sqrt{\\dfrac{r_{a}}{r_{c}}}$

$\\dfrac{v_{b}}{v_{c}}=\\sqrt{\\dfrac{r_{c}}{r_{b}}}$

$\\dfrac{\\omega_{a}}{\\omega_{c}}=\\sqrt{\\dfrac{r_{a}}{r_{c}}}$

$\\dfrac{\\omega_{b}}{\\omega_{c}}=\\sqrt{\\dfrac{r_{c}}{r_{b}}}$

由万有引力提供向心力$G\dfrac{Mm}{r^{2}} =m\dfrac{v^{2}}{r}=mr\omega^{2}$

可得$v=\sqrt{\dfrac{GM}{r}}$，$\omega=\sqrt{\dfrac{GM}{r^{3}}}$

则$\dfrac{v_{a}}{v_{c}}=\sqrt{\dfrac{r_{c}}{r_{a}}}$，$\dfrac{v_{b}}{v_{c}}=\sqrt{\dfrac{r_{c}}{r_{b}}}$，$\dfrac{\omega_{a}}{\omega_{c}}=\sqrt{\dfrac{r_{c}^{3}}{r_{a}^{3}}}$，$\dfrac{\omega_{b}}{\omega_{c}}=\sqrt{\dfrac{r_{c}^{3}}{r_{b}^{3}}}$

故选：$\rm B$。

若卫星$b$与卫星$c$质量相同，则卫星$b$的机械能$(\quad\ \ \ \ )$卫星$c$的机械能。

大于

等于

小于

规定无穷远处为零势能点，则卫星的机械能为$E=\dfrac{1}{2}mv^{2}+\left(-\dfrac{GMm}{r}\right)=- \dfrac{GMm}{2r}$

因为$r_{b}\gt r_{c}$

所以$E_{b}\gt E_{c}$

所以卫星$b$的机械能大于卫星$c$的机械能。

故选：$\rm A$。