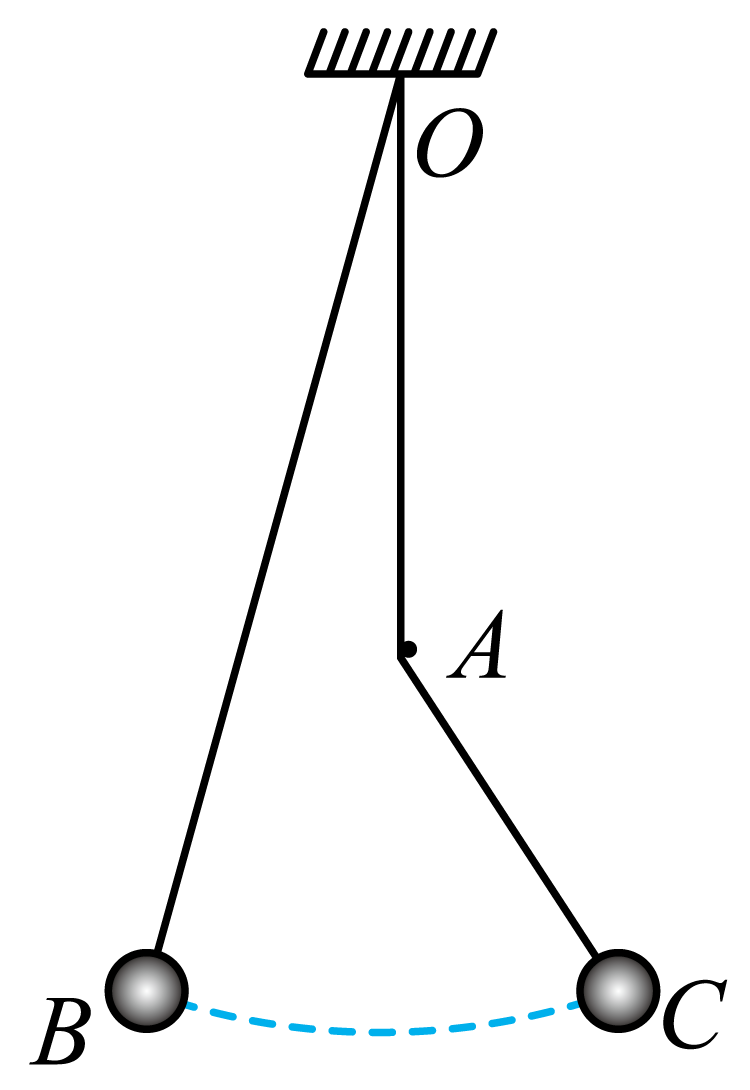
如图所示，在$O$点用长为$L$的细绳系着一小球，$O$点正下方$A$点处有一固定的光滑钉子，$AC=\dfrac{1}{4}L$。小球在$B$点由静止释放，运动至右侧最高点$C$点的时间为$t$，$AC$与竖直方向夹角足够小，重力加速度为$g$，不计空气阻力，则$t$可能等于$(\qquad)$

$3\\pi\\sqrt{\\dfrac{L}{g}}$

$\\dfrac{3\\pi}{2}\\sqrt{\\dfrac{L}{g}}$

$\\dfrac{15\\pi}{4}\\sqrt{\\dfrac{L}{g}}$

$\\dfrac{15\\pi}{8}\\sqrt{\\dfrac{L}{g}}$

小球摆动过程的摆长为$L$时，其周期为$T_{1}=2\pi\sqrt{\dfrac{L}{g}}$

小球摆长为$\dfrac{L}{g}$时，其周期为$T_{2}=2\pi\sqrt{\dfrac{L}{4g}}=\pi\sqrt{\dfrac{L}{g}}$

小球在$B$点由静止释放，摆动的周期为$T=\dfrac{1}{2}T_{1}+\dfrac{1}{2}T_{2}=\pi\sqrt{\dfrac{L}{g}}+\dfrac{\pi}{2}\sqrt{\dfrac{L}{g}}=\dfrac{3\pi}{2}\sqrt{\dfrac{L}{g}}$

小球在$B$点由静止释放，第一次运动至右侧最高点$C$点的时间为$t_{1}=\dfrac{1}{2}T=\dfrac{3\pi}{4}\sqrt{\dfrac{L}{g}}$

小球在$B$点由静止释放，运动至右侧最高点$C$点的时间为

$t=nT+t_{1}=\dfrac{3\pi n}{2}\sqrt{\dfrac{L}{g}}+\dfrac{3\pi}{4}\sqrt{\dfrac{L}{g}}$ $(n=0,1,2,3,⋯)$

当$n=0$时$t=\dfrac{3\pi}{4}\sqrt{\dfrac{L}{g}}$

当$n=1$时$t=\dfrac{9\pi}{4}\sqrt{\dfrac{L}{g}}$

当$n=2$时$t=\dfrac{15\pi}{4}\sqrt{\dfrac{L}{g}}$

故$\rm ABD$错误，$\rm C$正确。

故选：$\rm C$。