高中 | LC电磁振荡 题目答案及解析
稿件来源:高途
高中 | LC电磁振荡题目答案及解析如下,仅供参考!
选修3-4
第十四章 电磁波
14.2 电磁振荡
LC电磁振荡
中国高铁利用“北斗”导航技术、$\rm 5G$通信技术等构建运营的“超强大脑”,实现了数字化、智能化的管理。具有完全自主知识产权的新一代高速列车“复兴号”投入了高铁运营。
$\rm 5G$信号相较于$\rm 4G$信号采用了频率更高的无线电波,具有数据传输更快的特点。
①(多选)在空气中传播时,$\rm 5G$信号与$\rm 4G$信号相比 ;
$\rm A$.具有更快的传播速度 $\rm B$.具有相同的传播速度
$\rm C$.更容易发生衍射 $\rm D$.更不容易发生衍射
②(多选)无线电波可由$LC$振荡电路产生,某时刻的电路工作状态如图所示,此时 。
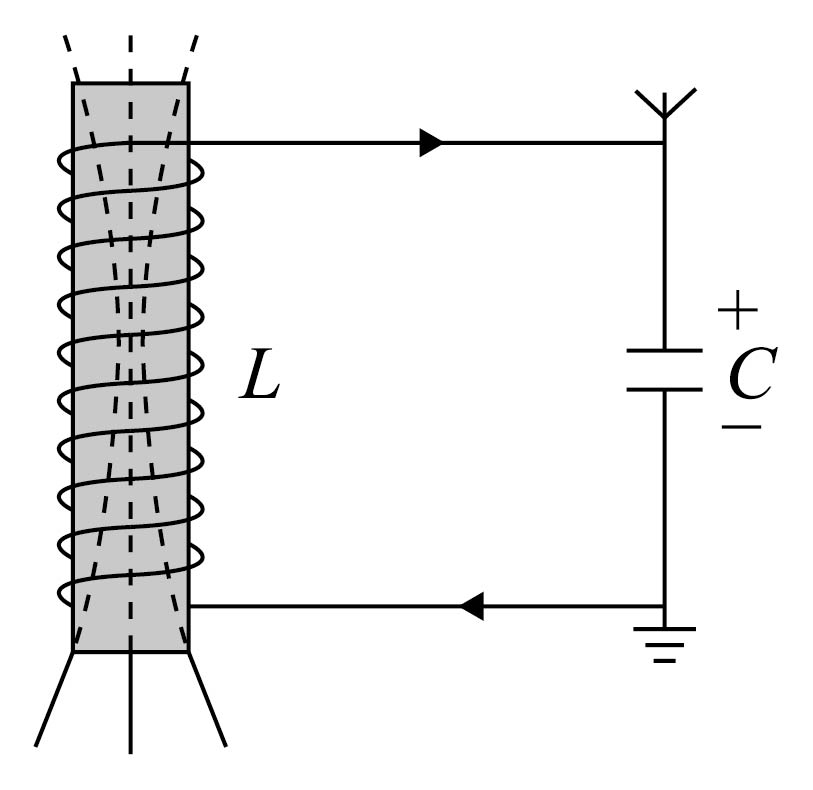
$\rm A$.电容器正在放电 $\rm B$.电容器正在充电
$\rm C$.线圈中磁场的方向向上 $\rm D$.线圈中磁场的方向向下
$\rm E$.线圈储存的磁场能正在增大 $\rm F$.线圈储存的磁场能正在减小
①$\rm AB$.在空气中传播时,$\rm 5G$信号与$\rm 4G$信号具有相同的传播速度,均为光速$c$,故$\rm A$错误,$\rm B$正确;
$\rm CD$.$\rm 5G$信号相较于$\rm 4G$信号采用了频率更高的无线电波,则$\rm 5G$信号的波长小于$\rm 4G$信号的波长,所以$\rm 5G$信号与$\rm 4G$信号更不容易发生衍射,故$\rm C$错误,$\rm D$正确。
故选:$\rm BD$。
②由题图可知电流方向由下极板流向上极板,且上极板带正电,则此时电容器正在充电;可知此时电容器电场能正在增大,线圈储存的磁场能正在减小;根据右手螺旋定则可知线圈中磁场的方向向上。
故选:$\rm BCF$。
“北斗”导航系统主要由地球同步轨道卫星和中轨道卫星组成。某一地球同步轨道卫星和一颗中轨道卫星在同一平面内环绕地球做匀速圆周运动、且绕行方向相同。如图($\rm a$)所示。
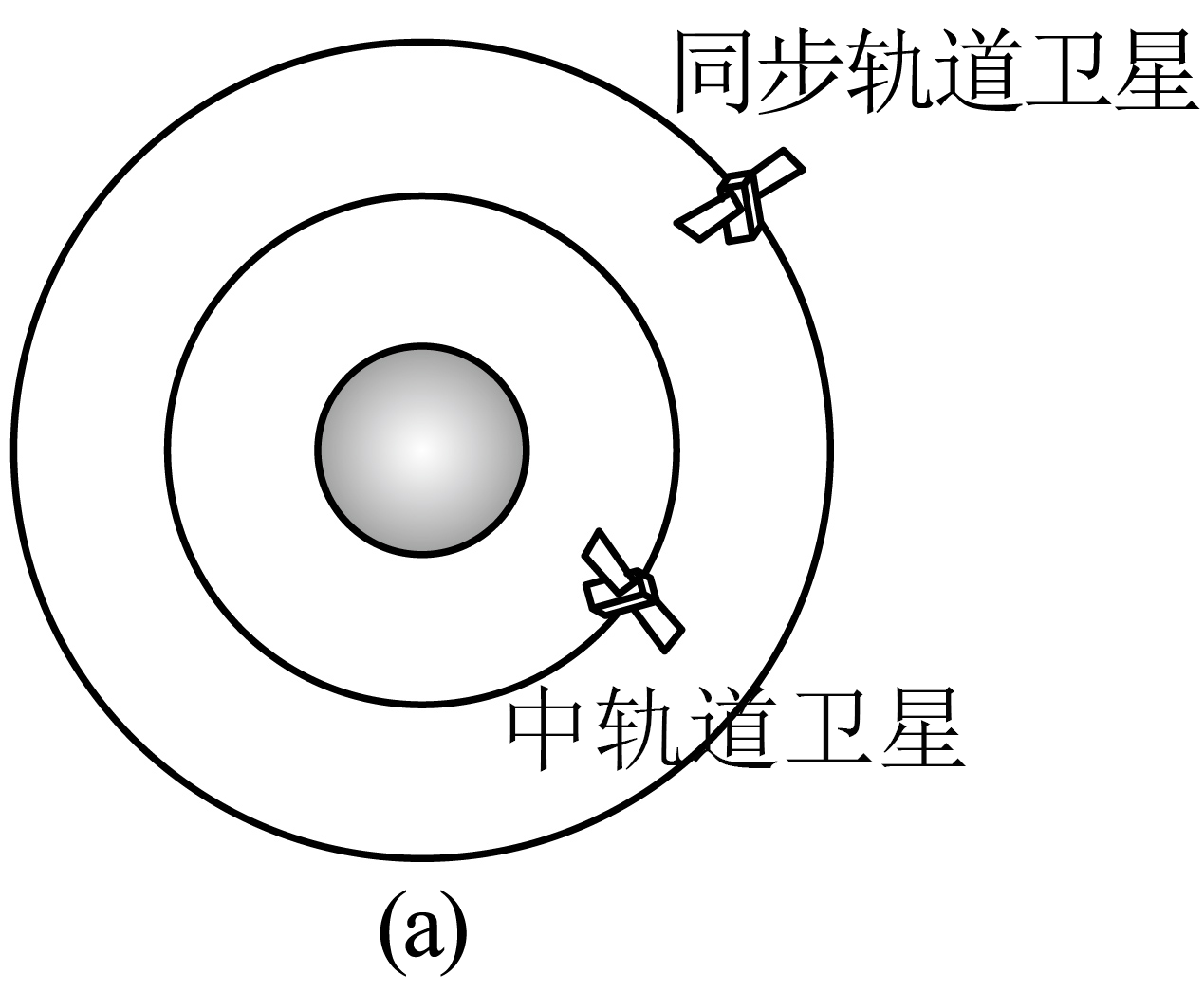
①同步轨道卫星和中轨道卫星绕地球做圆周运动的线速度分别$v_{1}$、$v_{2}$,则 ;
$\rm A$.$v_{1}\lt v_{2}$ $\rm B$.$v_{1}=v_{2}$ $\rm C$.$v_{1}\gt v_{2}$
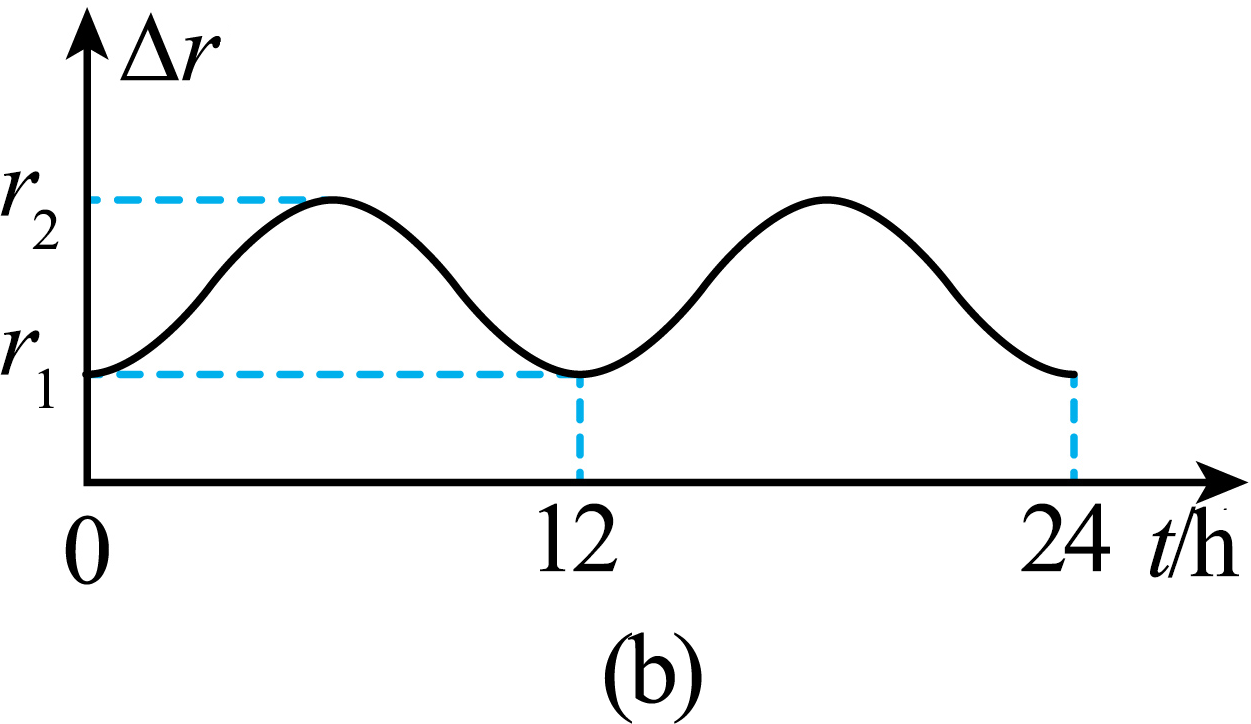
②若这两颗卫星之间的距离$\Delta r$随时间$t$变化的关系如图($\rm b$)所示,则中轨道卫星的运行周期$T=$ $\rm h$。
①卫星绕地球做匀速圆周运动,由万有引力提供向心力可得$\dfrac{GMm}{r^{2}}=m\dfrac{v^{2}}{r}$
可得$v=\sqrt{\dfrac{GM}{r}}$
由于同步轨道卫星半径大于中轨道卫星半径,则有$v_{1}\lt v_{2}$
故选:$\rm A$。
②由题图可知,两卫星每隔$\Delta t=12h$相距最近,则有$\left(\dfrac{2\pi}{T}-\dfrac{2\pi}{T_{同}}\right)\Delta t=2\pi$
可得中轨道卫星的运行周期为$T=\dfrac{\Delta t \cdot T_{同}}{\Delta t+T_{同}}=\dfrac{12 \times 24}{12+24}\ \text{h}=8\;\rm \text{h}$
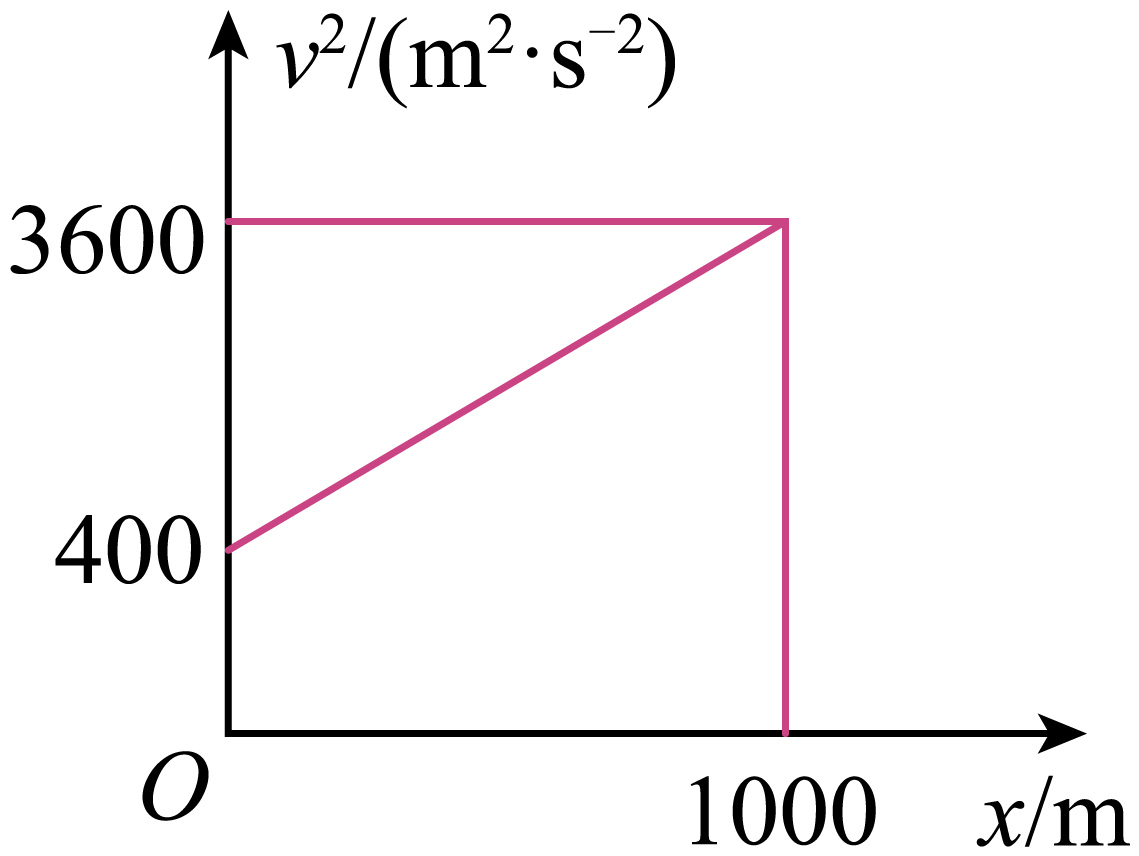
“复兴号”列车在某段长为$1000\;\rm m$的平直轨道上行驶,其速度的平方$v^{2}$与位移$x$的关系,如图所示。
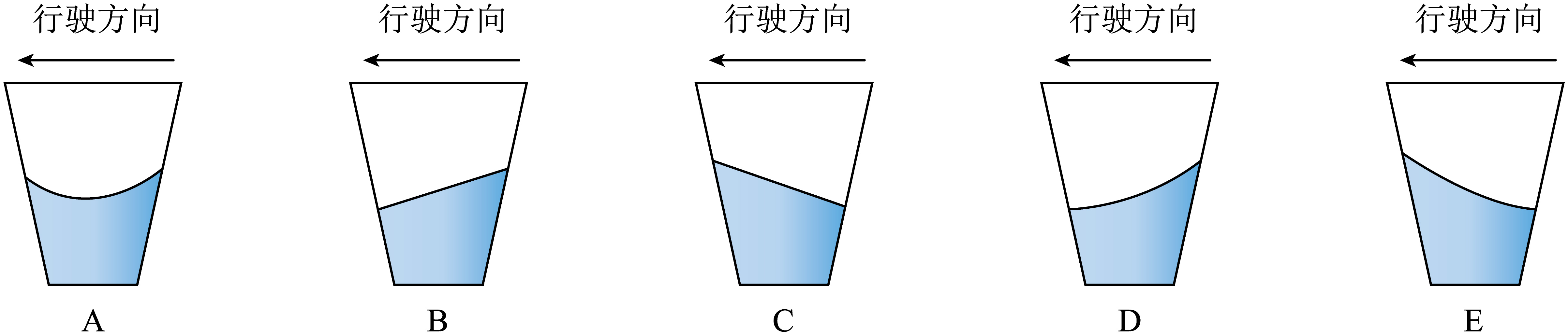
①乘客将一水杯放置在车厢水平桌面上,在此过程中水杯里水面的形状可能是 ;
②列车通过此路段所用的时间为 $\;\rm s$。
①根据$v^{2}-x$图像可知,列车做匀加速直线运动,加速度大小为$a=\dfrac{v^{2}-v_{0}^{2}}{2x}=\dfrac{3600- 400}{2 \times 1000}=1.6\;\rm \text{m}/\text{s}^{2}$
乘客将一水杯放置在车厢水平桌面上,设水面与水平方向的夹角为$\theta$,则有$mg\tan \theta=ma$
可得$\tan\theta=\dfrac{a}{g}$
可知此过程中水杯里水面的形状是一倾斜直线,且水的加速度方向与行驶方向相同。
故选:$\rm B$。
②由题图可知,$v_{0}=\sqrt{400}\;\rm \text{m}/\text{s}=20\;\rm \text{m}/\text{s}$,$v=\sqrt{3600}\;\rm \text{m}/\text{s}=60\;\rm \text{m}/\text{s}$
则列车通过此路段所用的时间为$t=\dfrac{v-v_{0}}{a}=\dfrac{60-20}{1.6}\ \text{s}=25\;\rm \text{s}$
如图,“复兴号”动车组共$8$节车厢。每节车厢的质量均为$m$,每节动力车厢能提供的最大驱动功率相同,重力加速度为$g$。

①(计算)动车组采用$4$动$4$拖模式,依靠前面的$4$节动力车厢来带动整个列车运行。动车组在平直轨道上匀加速启时,若每节车厢所受阻力均为车厢所受重力的$k$倍,每节动力车厢提供的牵引力大小为$F$,求第$4$节车厢对第$5$节车厢的作用力大小;
②若动车组在高速行驶过程中所受阻力与其速率成正比,采用$4$动$4$拖模式,最高时速可达$350\;\rm km/h$,则改为采用$1$动$7$拖模式后,动车组的最高时速为 $\;\rm km/h$。
①以$8$节车厢为整体,根据牛顿第二定律可得$4F-8kmg=8ma$
以后面$4$节车厢为整体,根据牛顿第二定律可得$F_{45}-4kmg=4ma$
联立解得第$4$节车厢对第$5$节车厢的作用力大小为$F_{45}=2F$
②若动车组在高速行驶过程中所受阻力与其速率成正比,采用$4$动$4$拖模式,最高时速可达$350\;\rm km/h$,则有$4P=fv_{\rm m}=kv_{\rm m}^{2}$
则改为采用$1$动$7$拖模式后,则$P=f'v'_{\rm m}=kv'^{2}_{{\rm m}}$
可得动车组的最高时速为${v'}_{\rm m}=\dfrac{1}{2}v_{\rm m}=\dfrac{1}{2} \times 350\;\rm \text{km}/\text{h}=175\;\rm \text{km}/\text{h}$
高速列车上安装有电磁制动系统,其原理可简单描述为线框进出磁场受电磁阻尼作用。某同学进行了模拟研究:用同种导线制成边长为$L$、质量为$m$的正方形线框$abcd$,将其放置在光滑绝缘的水平面内。线框$abcd$以初速度$v_{0}$进入磁感应强度大小为$B$、方向竖直向下,宽度为$d$的匀强磁场($d\gt L$),测得当线框完全穿过磁场时,其速度大小为$\dfrac{v_{0}}{2}$,如图所示。
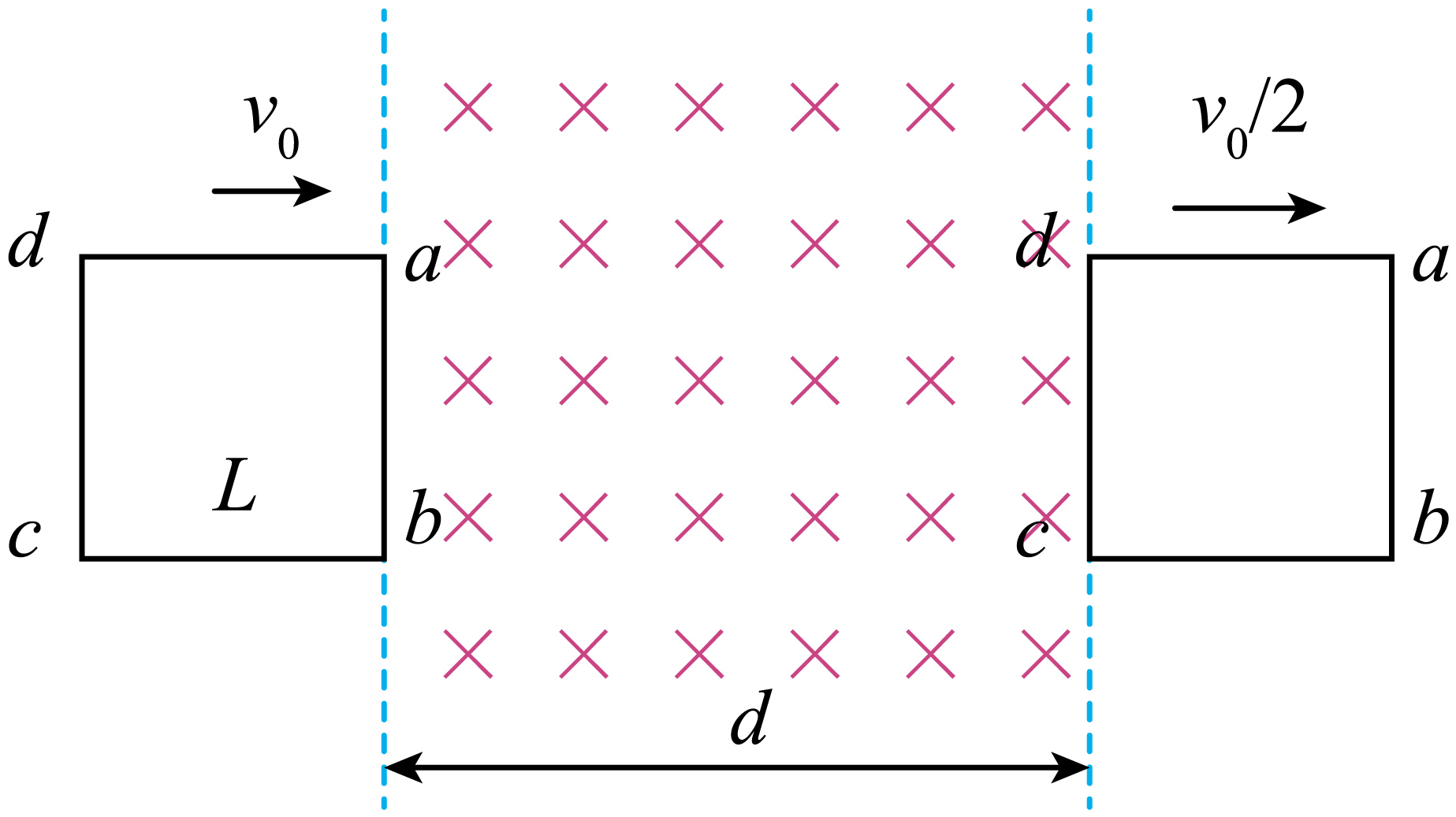
①线框$abcd$刚进入磁场和刚要离开磁场时,$ab$两点间的电势差分别为$U_{ab}$和$U'_{ab}$,则$U_{ab}:U'_{ab}=$ ;
②(计算)求线框$abcd$的电阻大小$R$;
③线框$abcd$在进入磁场和离开磁场的过程中,线框中产生的热量分别为$Q_{1}$和$Q_{2}$,则$Q_{1}:Q_{2}=$ 。
①设线框$abcd$的电阻为$R$,线框$abcd$刚进入磁场时,产生的电动势为$E=BLv_{0}$
此时$ab$两点间的电势差为$U_{ab}=I \cdot \dfrac{3}{4}R=\dfrac{E}{R} \cdot \dfrac{3}{4}R=\dfrac{3BLv_{0}}{4}$
线框$abcd$刚离开磁场时,产生的电动势为$E'=BL \cdot \dfrac{v_{0}}{2}$
此时$ab$两点间的电势差为${U'}_{ab}=I' \cdot \dfrac{1}{4}R=\dfrac{E'}{R} \cdot \dfrac{1}{4}R=\dfrac{BLv_{0}}{8}$
则有$U_{ab}:U'_{ab}=6:1$
②线框从进入磁场到离开磁场过程,根据动量定理可得$- \sum F_{安}t=m \cdot \dfrac{v_{0}}{2}-mv_{0}$
又$F_{安}=BIL=B\dfrac{E}{R}L=\dfrac{B^{2}L^{2}}{R}v$
则有$\sum F_{安}t=\sum\dfrac{B^{2}L^{2}}{R}vt=\dfrac{B^{2}L^{2}}{R}\sum vt=\dfrac{B^{2}L^{2}}{R} \cdot 2L$
联立解得线框$abcd$的电阻为$R=\dfrac{4B^{2}L^{3}}{mv_{0}}$
③设线框完全进入磁场时的速度大小为$v_{1}$,则线框进入磁场过程,根据动量定理可得$- \sum F_{安}t=- \dfrac{B^{2}L^{2}}{R} \cdot L=mv_{1}-mv_{0}$
线框离开磁场过程,根据动量定理可得$- \sum F_{安}t=- \dfrac{B^{2}L^{2}}{R} \cdot L=m \cdot \dfrac{v_{0}}{2}-mv_{1}$
解得$v_{1}=\dfrac{3}{4}v_{0}$
根据能量守恒可得$Q_{1}=\dfrac{1}{2}mv_{0}^{2}-\dfrac{1}{2}mv_{1}^{2}=\dfrac{7}{32}mv_{0}^{2}$,$Q_{2}=\dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}m{\left(\dfrac{v_{0}}{2}\right)}^{2}=\dfrac{5}{32}mv_{0}^{2}$
则有$Q_{1}:Q_{2}=7:5$
高中 | LC电磁振荡题目答案及解析(完整版)
