彩超通过发射和接收超声波成像。当血细胞向探头运动，接收到的反射波频率$(\quad\ \ \ \ )$。

变小

不变

变大

根据题意，由多普勒效应可知，当血细胞向探头运动，接收到的反射波频率变大。

故选：$\rm C$。

核磁共振设备的冷头工作时，氦气经历周期性压缩与膨胀。如图$A→B→C→A$是一定质量氦气的压强$p$随体积$V$的变化图像。已知$A$点温度为$T$，则$B$点温度为                 ；由状态$C$到状态$A$的过程中，系统放出的热量为                 。

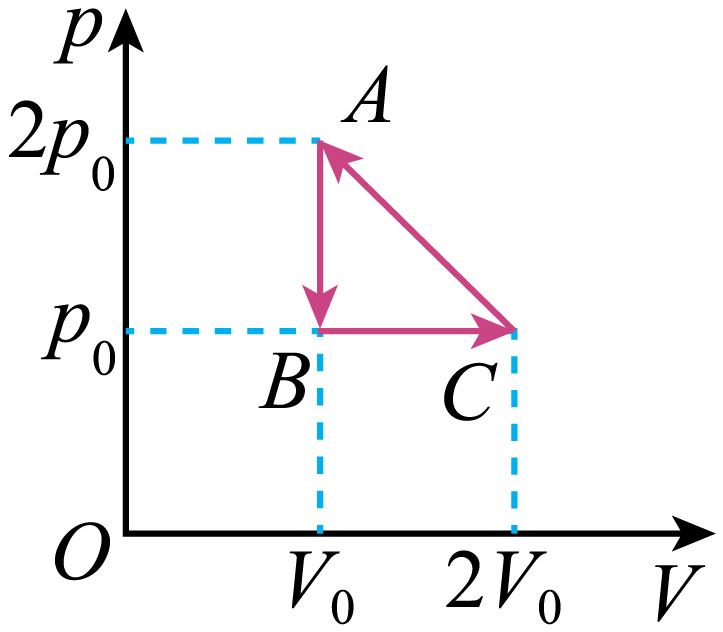
由图可知，从$A$到$B$过程中，气体做等容变化，则有$\dfrac{p_{A}}{T_{A}}= \dfrac{p_{B}}{T_{B}}$

解得$T_{B}=\dfrac{p_{0}}{2p_{0}} \cdot T=\dfrac{T}{2}$

由状态$C$到状态$A$的过程中，由理想气体状态方程有$\dfrac{p_{A}V_{A}}{T_{A}}=\dfrac{p_{C}V_{C}}{T_{C}}$

可得$T_{A}=T_{C}$

则气体在状态$A$和状态$C$的内能相等，气体体积减小，外界对气体做功，大小为$W=\dfrac{1}{2}\left( p_{0}+2p_{0} \right)\left( 2V_{0}-V_{0} \right)=\dfrac{3}{2}p_{0}V_{0}$

由热力学第一定律可知，系统放出的热量为$Q=W=\dfrac{3}{2}p_{0}V_{0}$

正电子发射断层扫描（$\rm PET$）是一种基于放射性同位素衰变的核医学成像技术，它的基本原理是：将放射性示踪剂$\rm _{9}^{18}F$注入人体，$\rm _{9}^{18}F$在人体内衰变放出正电子。

①$\rm _{9}^{18}F$的衰变方程为                 。

②如图为$\rm _{9}^{18}F$在$0\sim 100\;\rm \min$的衰变图像画出$100\sim 300\;\rm \min$的图像（横坐标$t$表示时间，纵坐标$\dfrac{N}{N_{0}}$表示任意时刻$\rm _{9}^{18}F$的原子数$N$与$t=0$时的原子数$N_{0}$之比）                 。

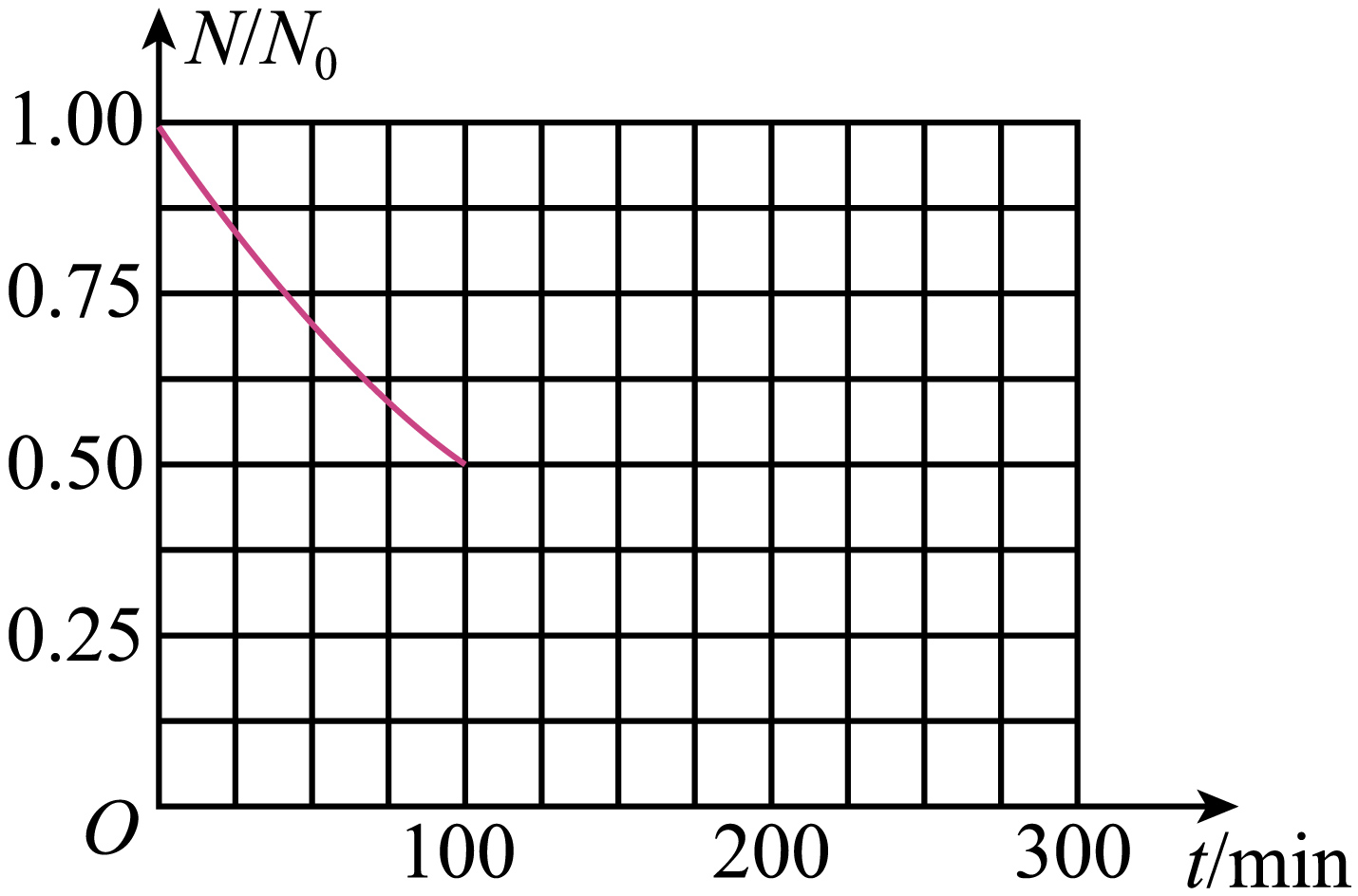
根据题意，由质量数守恒和电荷数守恒可得$\rm _{9}^{18}F$的衰变方程为$\rm _{9}^{18}F→_{8}^{18}O+_{1}^{0}e$。

根据题意，结合图像可知，$\rm _{9}^{18}F$的半衰期为$100\;\rm \min$，画出$100\sim 300\;\rm \min$的图像如图所示

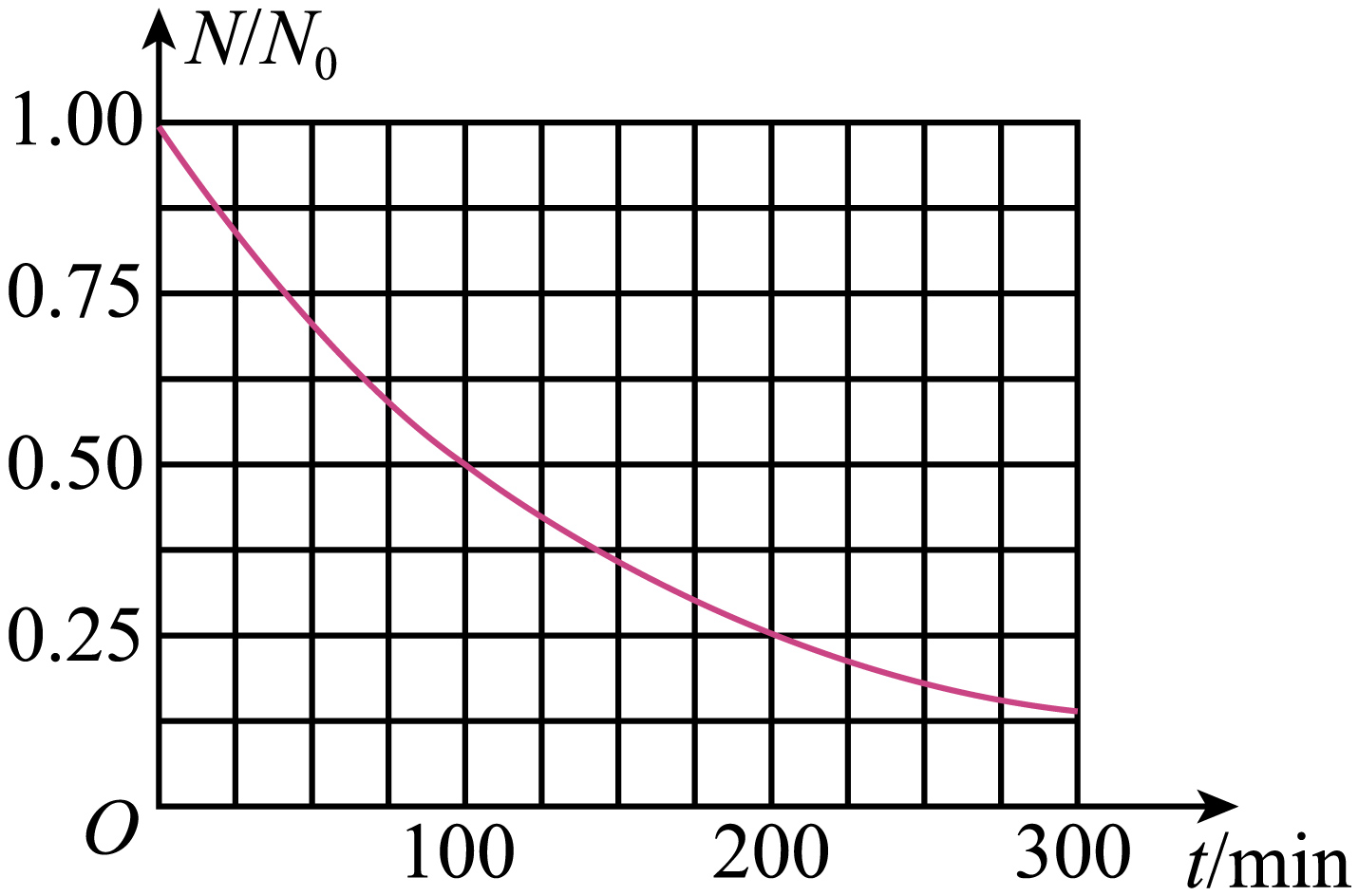
（计算）如图为磁屏蔽室中的某种扫描机，$M$、$N$之间是加速电场，长方形虚线框内存在垂直纸面的匀强磁场。正电子从静止开始经电场加速后，垂直边界进入磁场，在磁场中的速度偏转的角度为$\theta$ ，最后打在靶上的$P$点。已知加速电压为$U=200\;\rm V$，磁场宽度$d=0.1\;\rm m$，正电子质量$m=9.1 \times 10^{-31}\;\rm kg$、电荷量$e=1.6 \times 10^{-19}\;\rm C$，偏转角为$\theta=30^\circ $，求：（保留$3$位有效数字）。

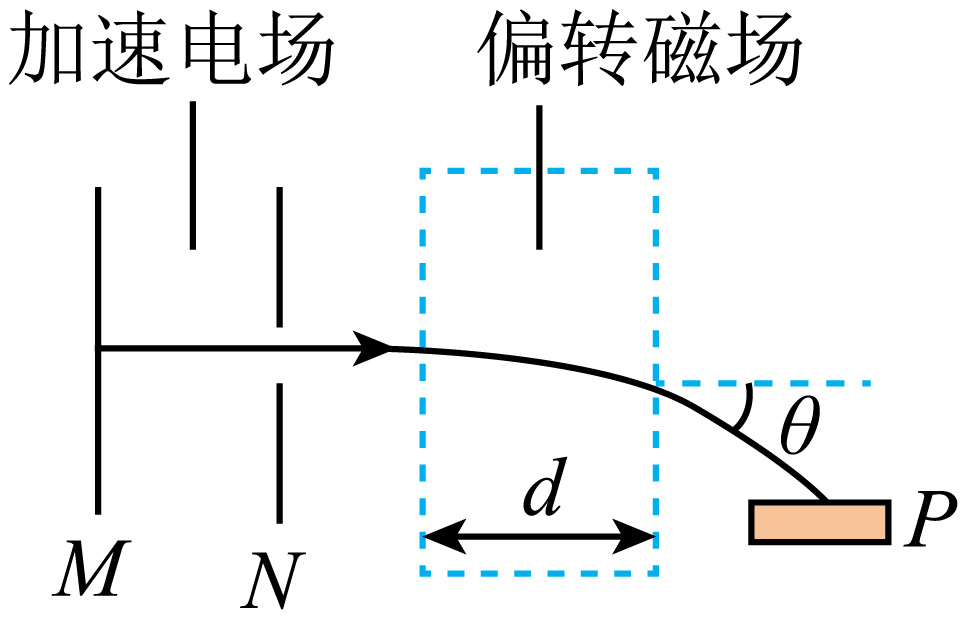
正电子离开电场时的速度大小；

偏转磁场的磁感应强度$B$。

①$8.39 \\times 10^{6}\\ {\\text{m}}/{\\text{s}}$；②$2.39 \\times 10^{-4}\\;\\rm T$，方向垂直直面向外

①根据题意可知，正电子在电场中加速，由动能定理有$eU=\dfrac{1}{2}mv_{0}^{2}$

解得正电子离开电场时的速度大小$v_{0}=\sqrt{\dfrac{2eU}{m}} \approx 8.39 \times 10^{6}\ {\text{m}}/{\text{s}}$

②根据题意可知，正电子进入磁场后，做匀速圆周运动，运动轨迹如图所示

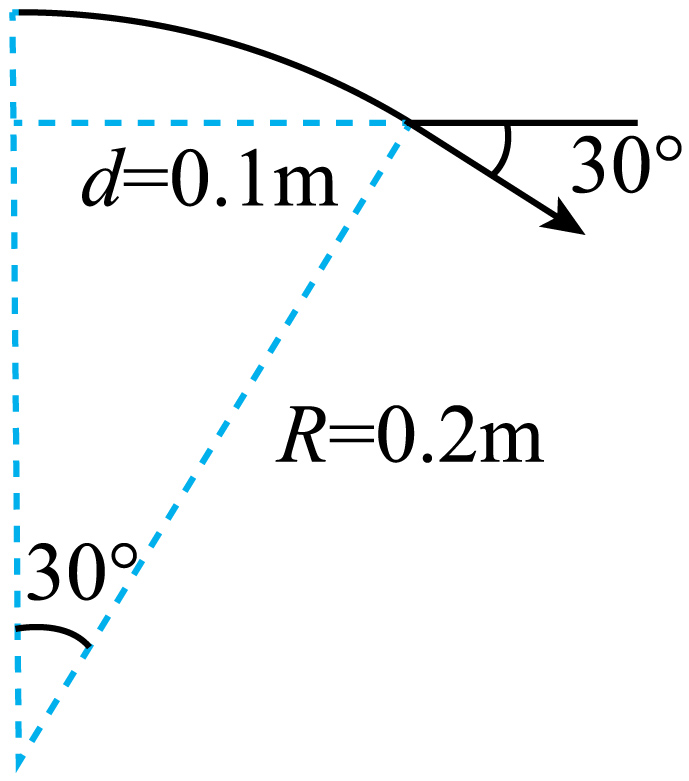
由几何关系可得$R=\dfrac{d}{\sin 30{^\circ}}=2d=0.2\;\rm \text{m}$

由洛伦兹力提供向心力有$ev_{0}B=m\dfrac{v_{0}^{2}}{R}$

解得$B\approx 2.39 \times 10^{-4}\;\rm T$

由左手定则可判断得出磁感应强度方向垂直直面向外。