高中 | 气体的等容变化 题目答案及解析
稿件来源:高途
高中 | 气体的等容变化题目答案及解析如下,仅供参考!
选修3-3
第八章 气体
8.2 气体的等容变化和等压変化
气体的等容变化
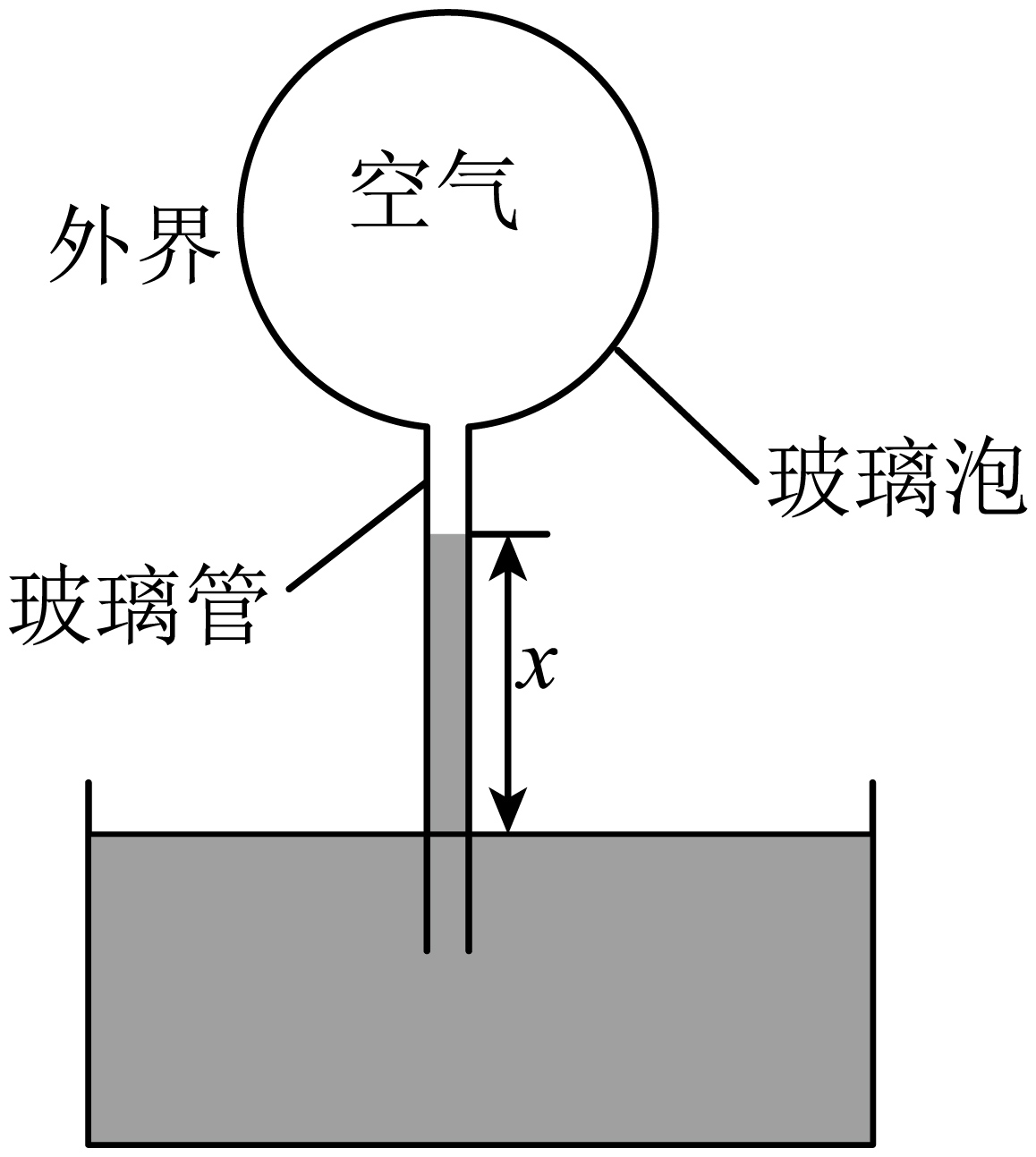
有人设计了一种如图所示的测温装置,玻璃管的上端与导热良好的玻璃泡连通,玻璃泡中封有一定量的气体,玻璃管下端插入水银中,通过管内水银面的高度$x$即可反映泡内气体的温度,即环境温度。已知在标准大气压为$76\;\rm cmHg$的环境下,热力学温度$T_{1}=300\;\rm K$时,玻璃管内水银面的高度为$x=20.0\;\rm cm$。假设玻璃管的体积与玻璃泡的体积相比可略去不计。
若玻璃管内水银面的高度为$22.8\;\rm cm$,求环境的热力学温度;
$285\\;\\rm K$;
"]]由题意可知,该过程为等容变化,初状态$p_{1}=76\;\rm cmHg − 20\;\rm cmHg=56\;\rm cmHg$,$T_{1}=300\;\rm K$
末状态$p_{2}=76\;\rm cmHg − 22.8\;\rm cmHg=53.2\;\rm cmHg$
根据查理定律则有$\dfrac{p_{1}}{T_{1}}=\dfrac{p_{2}}{T_{2}}$
代入数据解得$T_{2}=285\;\rm K$;
某同学将该装置拿到黄山某山峰顶,环境的热力学温度为$285\;\rm K$,他发现管内水银面的高度为$7.3\;\rm cm$,通过计算估算该山峰的海拔。(已知海拔$3000\;\rm m$以内,每升高$120\;\rm m$,大气压减小约$1\;\rm cmHg$)
$1860\\;\\rm m$。
"]]由题意可知,该过程为等容变化,初状态$p_{1}=76\;\rm cmHg − 20\;\rm cmHg=56\;\rm cmHg$,$T_{1}=300\;\rm K$
末状态$p_{3}=p − 7.3\;\rm cmHg$,$T_{3}=285\;\rm K$
根据查理定律则有$\dfrac{p_{1}}{T_{1}}=\dfrac{p_{3}}{T_{3}}$
解得$p=60.5\;\rm cmHg$
该山峰的海拔高度为$h=(76 − 60.5) \times 120\;\rm m=1860\;\rm m$。
高中 | 气体的等容变化题目答案及解析(完整版)
