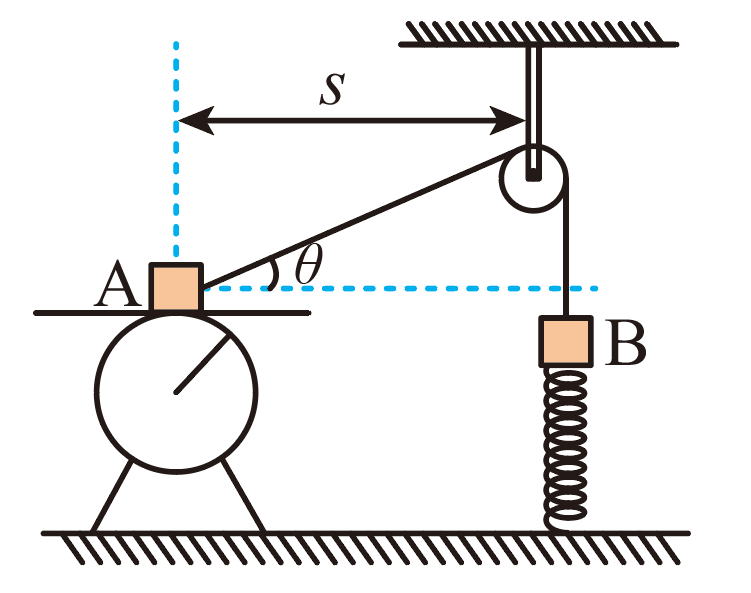
求物块$A$受到的摩擦力和绳对物块$A$的拉力；

$T=2\\;\\rm N$，$f=1.6\\;\\rm N$

由台式测力计的示数知物块$A$此时所受的支持力$F_{N}=8.8\;\rm N$，物块$A$受力示意图如图所示。

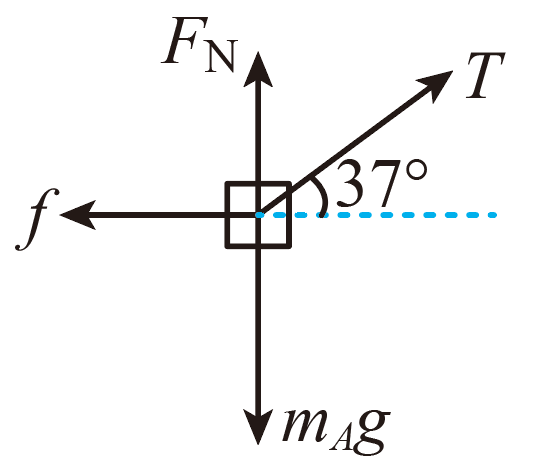
根据平衡条件可知$T\cos37^\circ-f=0$，$F_{N}+T\sin37{^\circ}-m_{A}g=0$

解得$T=2\;\rm N$，$f=1.6\;\rm N$

沿竖直方向调整滑轮的高度至某一位置时，物块$A$刚好运动，且此时弹簧刚好离开地面，求滑轮移动的距离和弹簧的劲度系数（整个过程中台式测力计的水平台高度不变）。

$\\Delta h=\\dfrac{\\text{35}}{\\text{3}}\\;\\text{cm}$；$k=15\\;\\rm N/m$

分析可知，此时弹簧恢复原长，弹力为零；对$B$进行受力分析，有$T_{1}-m_{B}g=0$

故$T_{1}=5\;\rm N$

设此时轻绳与水平方向夹角为$\theta'$，对$A$有

$T'_{1}\cos\theta'-f_{m}=0$，$F_{N1}+T'_{1}\sin\theta'-m_{A}g=0$

又$f_{m}=\mu F_{N1}$，$T_{1}=T'_{1}$

解得$\sin\theta^{^\prime}=0.8$，$\cos\theta^{^\prime}=0.6$

滑轮上升的高度$\Delta h=s\tan\theta'-s\tan\theta=\dfrac{\text{35}}{\text{3}}\;\text{cm}$

由分析知，右端绳缩短$\Delta l=\dfrac{s}{\cos\theta'}-\dfrac{s}{\cos\theta}=\dfrac{\text{25}}{\text{3}}\;\text{cm}$

由几何关系可知，弹簧伸长量$\Delta x=\Delta h+\Delta l=20\;\rm cm$

结合（$1$）问，对$B$进行受力分析，初始时刻弹簧处于压缩状态，弹力为$3\;\rm N$；弹簧刚好离开地面时，弹簧恢复原长，弹力为零，所以$k=\dfrac{\Delta F}{\Delta x}=\dfrac{{3\;\rm N}}{{20\;\rm cm}}=15\;\rm N/m$