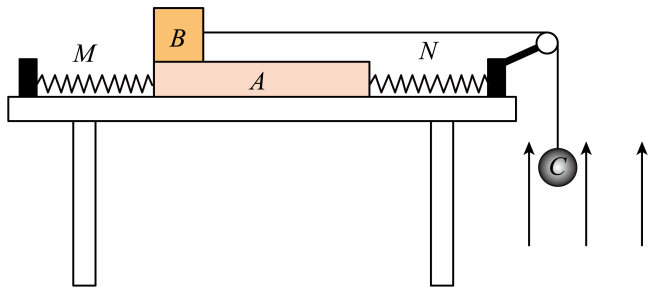
求匀强电场的场强大小；

$2 \\times 10^{6}\\;\\rm N/C$；

撤去电场前，$A$、$B$、$C$均静止，$M$、$N$处于原长状态，对$A$、$B$整体分析可知，此时绳中拉力为$0$，对$C$根据共点力平衡条件有$qE=m_{C}g$

解得$E=2 \times 10^{6}\;\rm N/C$；

求$A$与$B$间的滑动摩擦因数及$C$做匀速运动时的速度大小；

$0.5$；$\\dfrac{2}{3}\\:\\rm{m/s}$；

$C$开始做匀速直线运动后，对$C$和$B$根据共点力平衡条件分别有

$T_{1}=m_{C}g$，$T_{1}=f_{B}$

其中$f_{B}=\mu m_{B}g$

解得$\mu =0.5$

$C$开始匀速运动瞬间，$A$、$B$刚好发生相对滑动，此时$A$、$B$、$C$三者速度大小相等，$M$、$N$两弹簧的弹性势能相同，$C$下降$0.2m$的过程中，对$A$、$B$、$C$及弹簧$M$、$N$组成的系统，由能量守恒定律有$m_{{C}}gh=\dfrac{1}{2}(m_{{A}}+m_{{B}}+m_{{C}})v^{2}+2E_{\rm{p}}$

解得$v=\dfrac{2}{3}\:\rm{m}/{s}$；

若$t=0$时电场方向改为竖直向下，当$B$与$A$即将发生相对滑动瞬间撤去电场，$A$、$B$继续向右运动，一段时间后，$A$从右向左运动。求$A$第一次从右向左运动过程中最大速度的大小。（整个过程$B$未与$A$脱离，$C$未与地面相碰）

$\\dfrac{2}{3}\\sqrt{2}\\;\\rm {m/s}$。

没有电场时，$C$开始匀速运动瞬间，$A$、$B$刚好发生相对滑动，所以此时$A$的加速度为零，对$A$根据共点力平衡有$2kh − f=0$

当电场方向改为竖直向下，设$B$与$A$即将发生相对滑动时，$C$下降高度为$h'$，对$A$根据牛顿第二定律可得$f'− 2kh'=m_{A}a$

对$B$、$C$根据牛顿第二定律可得$qE+m_{C}g − f=(m_{B}+m_{C})a$

撤去电场后，由第（$2$）问的分析可知$A$、$B$在$C$下降$0.2m$时开始相对滑动，在$C$下降$0.2m$的过程中，对$A$、$B$、$C$及弹簧$M$、$N$组成的系统，由能量守恒定律有$qEh'+m_{{C}}gh=\dfrac{1}{2}(m_{{A}}+m_{{B}}+m_{{C}})v_{\rm\max}^{2}+2E_{\rm{p}}$

此时$A$的速度是其从左向右运动过程中的最大速度，此后$A$做简谐运动，所以$A$第一次从右向左运动过程中的最大速度为$v'_{\rm\max}=v_{\rm\max}$

联立解得${v'}_{\rm\max}=\dfrac{2\sqrt{2}}{3}\:\rm{m/s}$。