高中 | 双棒模型 题目答案及解析
稿件来源:高途
高中 | 双棒模型题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.4 法拉第电磁感应定律
双棒模型
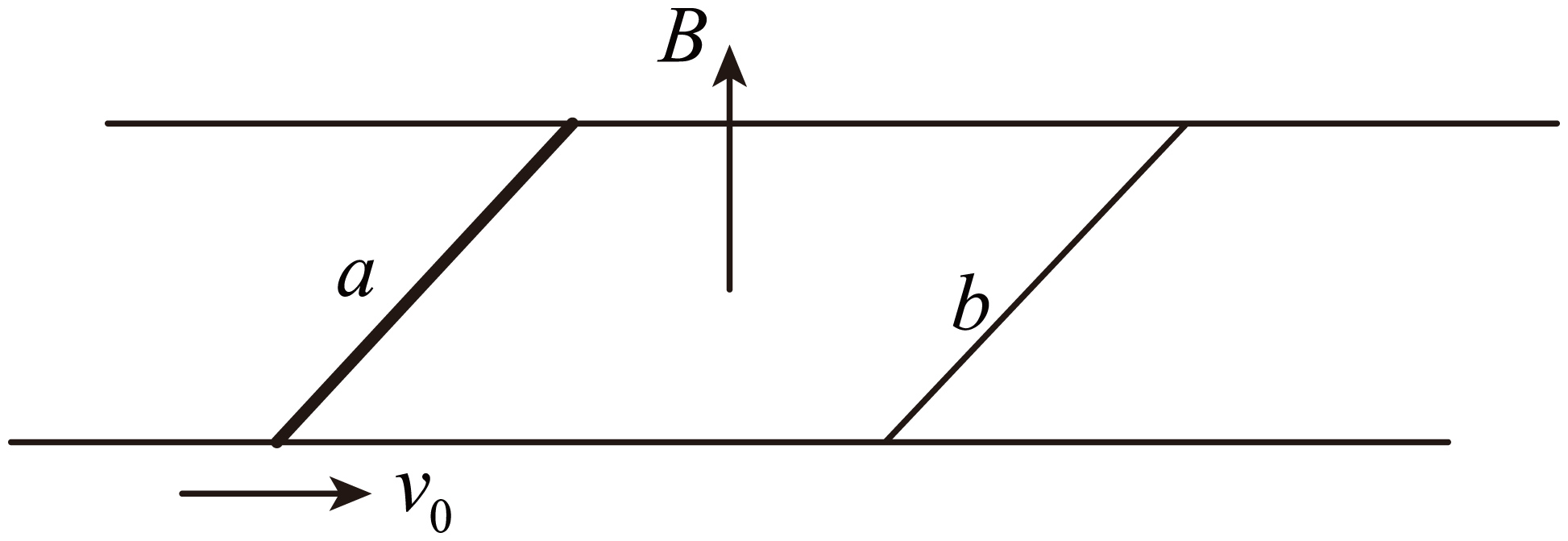
如图,足够长的平行光滑金属导轨固定在水平桌面上,间距$L=0.5\;\rm \text{m}$,处在磁感应强度$B=2\;\rm \text{T}$、竖直向上的匀强磁场中。质量${{m}_{1}}=0.4\;\rm \text{kg}$、电阻${r}=0.4\;\rm \Omega $的导体棒$a$长度与导轨间距相等,垂直导轨放置。质量$m_{2}=0.6\;\rm {kg}$、电阻${{r}_{2}}=0.6\;\rm \Omega $的导体棒$b$与$a$等长,垂直导轨静止在$a$的右侧某一位置处。现使$a$以初速度${{v}_{0}}=10\;\rm \text{m/s}$向右运动,$a$、$b$未发生碰撞。导体棒和导轨接触良好,导轨电阻不计。求:
从开始运动到两棒到达稳定状态,导体棒$a$上产生的焦耳热;
$4.8\\;\\rm J$;
"]]导体棒$a$与导体棒$b$组成的系统满足动量守恒,则有${{m}_{1}}{{v}_{0}}=({{m}_{1}}+{{m}_{2}})v$
解得$v=4\;\rm m/s$
根据能量守恒可得${{Q}_{总}}=\dfrac{1}{2}{{m}_{1}}v_{0}^{2}-\dfrac{1}{2}({{m}_{1}}+{{m}_{2}}){{v}^{2}}$
解得${{Q}_{总}}=12\;\rm \text{J}$
则导体棒$a$上产生的焦耳热为${{Q}_{a}}=\dfrac{{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}{{Q}_{总}}=\dfrac{2}{5}{{Q}_{总}}$
解得${{Q}_{a}}=4.8\;\rm \text{J}$;
初始时刻$a$、$b$棒的最小距离。
$2.4\\;\\rm \\text{m}$。
"]]对导体棒$b$应用动量定理得$B\bar{I}L\cdot \Delta t=m_{2}v$
又$q=\overline{I}\Delta t=\dfrac{\overline{E}}{{{r}_{1}}+{{r}_{2}}}\Delta t=\dfrac{\dfrac{\Delta \Phi }{\Delta t}}{{{r}_{1}}+{{r}_{2}}}\Delta t=\dfrac{\Delta \Phi }{{{r}_{1}}+{{r}_{2}}}=\dfrac{BLx}{{{r}_{1}}+{{r}_{2}}}$
联立解得$x=2.4\;\rm \text{m}$
则初始时刻$a$、$b$棒的最小距离为$2.4\;\rm \text{m}$。
高中 | 双棒模型题目答案及解析(完整版)
