如图所示，两段足够长的光滑平行金属导轨水平放置，导轨左右两部分的间距分别为$l$、$2l$；空间存在竖直向上的匀强磁场，磁感应强度大小为$B$，质量分别为$m$、${2 m}$的导体杆$a$、$b$均垂直导轨放置，接入电路的电阻分别为$R$、$2R$，导轨电阻忽略不计；$a$、$b$两杆同时分别以${{v}_{0}}$、$2{{v}_{0}}$的初速度向右运动，$a$总在左边窄导轨上运动，$b$总在右边宽导轨上运动，从开始运动到两杆稳定的过程中，下列说法正确的是$(\qquad)$

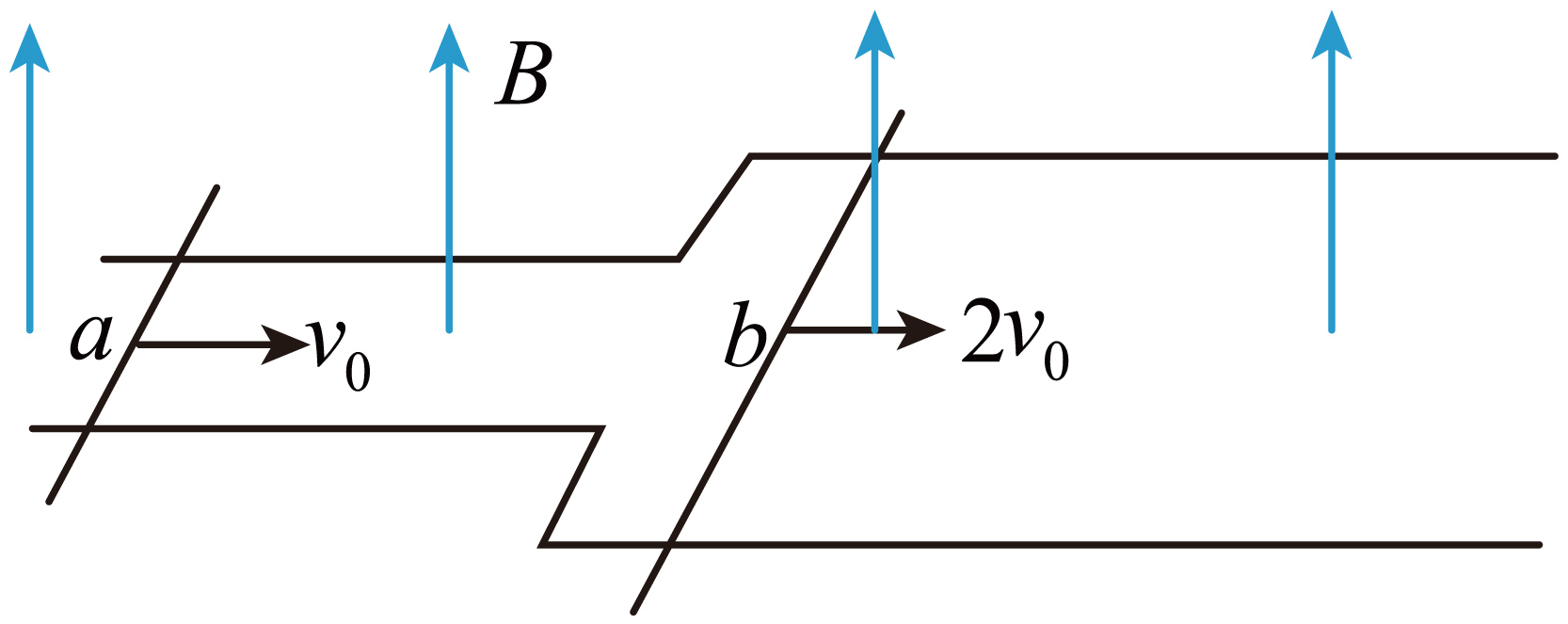
$a$杆加速度与$b$杆的加速度相同

稳定时$a$杆的速度为$2{{v}_{0}}$

电路中$a$杆上产生的焦耳热为$\\dfrac{3}{2}mv_{0}^{2}$

通过导体杆$a$的某一横截面的电荷量为$\\dfrac{mv_{0}}{Bl}$

$\rm A$．感应电流大小相等，根据牛顿第二定律有$BIl=2m{{a}_{a}}$，$BI\cdot 2l=2m{{a}_{b}}$

可知，加速度大小相等，根据右手定则可知，从上往下看，感应电流方向沿顺时针方向，根据左手定则可知，$a$受到的安培力方向向右，$b$受到的安培力方向向左，安培力方向相反，则加速度方向相反，可知，$a$杆加速度与$b$杆的加速度不相同，故$\rm A$错误；

$\rm B$．稳定时，感应电流为$0$，回路总的感应电动势为$0$，则有$B\cdot2lv_{b}=Blv_{a}$

对$a$杆，根据动量定理有$B\overline{I}l\Delta t=m{{v}_{a}}-m{{v}_{0}}$

对$b$杆，根据动量定理有$-B\overline{I}\cdot 2l\Delta t=2m{{v}_{b}}-2m\cdot 2{{v}_{0}}$

解得${{v}_{a}}=2{{v}_{0}}$，${{v}_{b}}={{v}_{0}}$，故$\rm B$正确；

$\rm D$．根据电流的定义式有$\overline{I}=\dfrac{q}{\Delta t}$

结合上述解得$q=\dfrac{m{{v}_{0}}}{Bl}$，故$\rm D$正确；

$\rm C$．回路产生的总的焦耳热$Q=\dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{2}\times2m\left( 2v_{0}\right)^{2}-\dfrac{1}{2}mv_{a}^{2}-\dfrac{1}{2}\times2mv_{b}^{2}$

电路中$a$杆上产生的焦耳热${{Q}_{a}}=\dfrac{QR}{R+2R}$

解得${{Q}_{a}}=\dfrac{1}{2}mv_{0}^{2}$，故$\rm C$错误。

故选：$\rm BD$。