高中 | 双棒模型 题目答案及解析
稿件来源:高途
高中 | 双棒模型题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.4 法拉第电磁感应定律
双棒模型
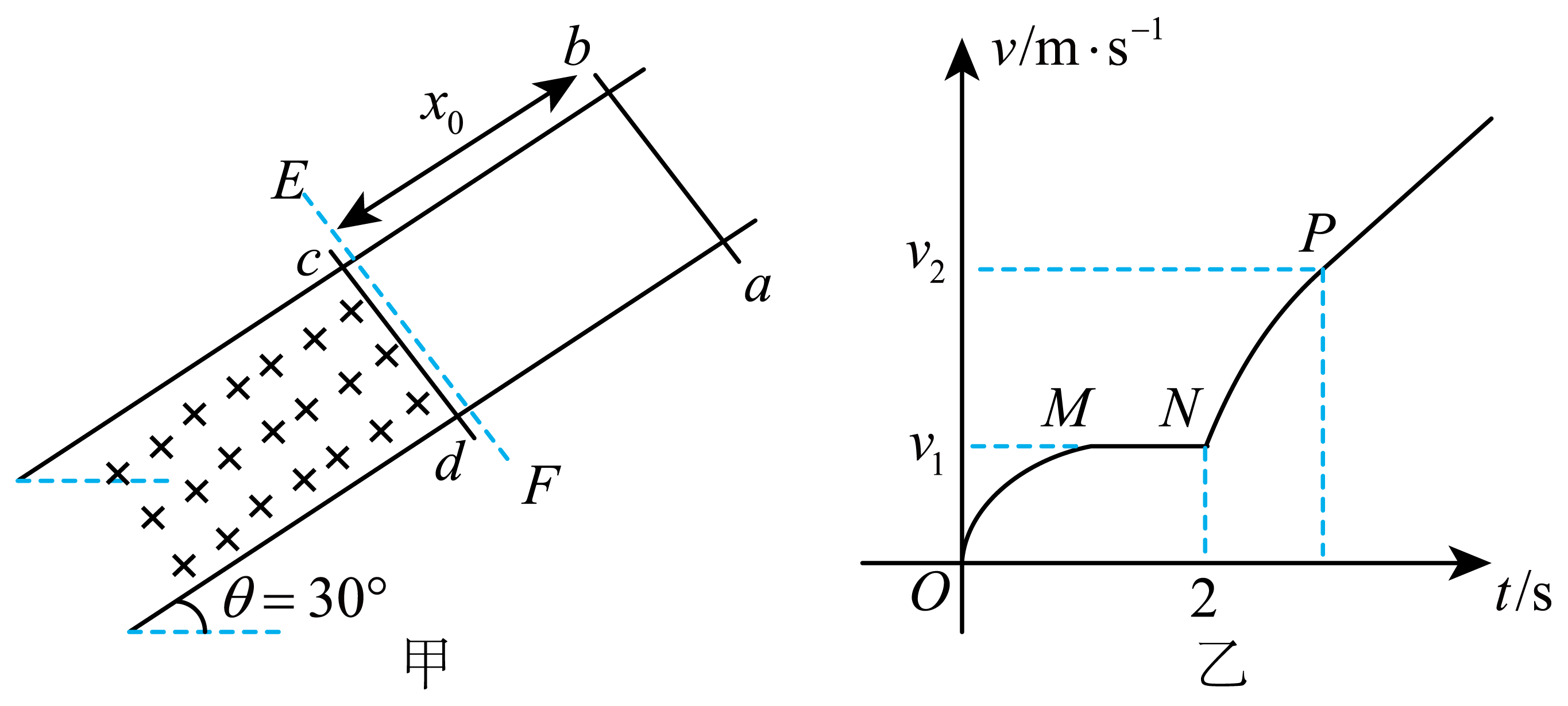
如图甲所示,粗细均匀的无限长光滑平行导轨固定在倾角$\theta =30^\circ $的斜面上,在边界$EF$下方区域存在垂直导轨平面向下的匀强磁场$B$,有两根相同金属棒$ab$、$cd$分别从磁场边界$EF$上方${{x}_{0}}=10\;\rm \text{m}$位置和边界$EF$位置同时由静止释放,$cd$棒运动的$v-t$图像如图乙所示,其中$OM$、$NP$段为曲线,其它段为直线。已知磁感应强度$B=4 \;\rm T$,导轨间距$L=0.5\;\rm \text{m}$,导体棒的质量均为$m=0.2\;\rm \text{kg}$,导体棒电阻均为$R=2\;\rm \Omega $,导轨电阻不计,$g$取$10\;\rm \text{m}/{{\text{s}}^{2}}$。求:
${{v}_{1}}$的大小并直接写出$ab$棒在整个运动过程中加速度的最大值;
${{v}_{1}}=1\\;\\rm {m/s }$,${{a}_{\\max}}=40\\;\\rm \\text{m/}{{\\text{s}}^{2}}$;
"]]设$2\;\rm s$前$cd$达到匀速直线运动时的速度为${{v}_{1}}$,$cd$棒受平衡力$B I_{1} L=m g \sin \theta$
代入题中数据,解得${{I}_{1}}=0.5\;\rm A$
因为${{I}_{1}}=\dfrac{BL{{v}_{1}}}{2R}$
联立解得${{v}_{1}}=1\;\rm \text{m/s}$
$2\;\rm s$时$ab$棒刚好进入磁场${{v}_{a}}=a{{t}_{1}}={10\;\rm m/s}$
电路中的感应电流${{I}_{2}}=\dfrac{BL{{v}_{a}}-BL{{v}_{1}}}{2R}$
对$ab$棒根据牛顿第二定律$B{{I}_{2}}L-mg\sin \theta =m{{a}_{\max }}$
可得$ab$棒在整个运动过程中加速度的最大值${{a}_{\max}}=40\;\rm \text{m/}{{\text{s}}^{2}}$;
从$t=0$到$t=2\;\rm s$导体棒$cd$位移大小${{x}_{cd}}$;
${{x}_{cd}}=1.8\\;\\rm \\text{m}$;
"]]$cd$棒在$0\sim 2\;\rm s$的运动过程,以${{v}_{1}}$的方向为正方向,由动量定理得$mg\sin \theta \times {{t}_{1}}-\underset{{}}{\overset{{}}{\mathop{\sum }}}\,BiL\Delta t=m{{v}_{1}}$
因为$q=i\Delta t$
因为$q=\bar{I}\Delta t=\dfrac{{\bar{E}}}{2R}\Delta t=\dfrac{\dfrac{\Delta\!\!\Phi}{\Delta t}}{2R}\Delta t=\dfrac{BL{{x}_{cd}}}{2R}$
联立解得${{x}_{cd}}=1.8\;\rm \text{m}$;
导体棒$ab$进入磁场后,通过导体棒$ab$的电荷量$q _ { 1 }$。
$0.45\\;\\rm C$。
"]]$ab$棒先做匀加速直线运动,由牛顿第二定律得$mg\sin =ma$
$2\;\rm s$时$ab$棒刚好进入磁场,其速度大小$va=at_{1}$
设$ab$棒进入磁场后经过时间$t _ { 2 }$与$cd$棒速度相等,一起做匀加速直线运动,以${{v}_{1}}$的方向为 正方向,则对$cd$棒有$mg\sin \theta \times {{t}_{2}}+\sum BLi'\Delta {{t}_{2}}=m{{v}_{2}}-m{{v}_{1}}$
以沿斜面向下的方向为正方向,对$ab$棒有$mg\sin \theta \times {{t}_{2}}-\sum BL{i}'\Delta {{t}_{2}}=m{{v}_{2}}-m{{v}_{a}}$
因为${{q}_{1}}=\underset{{}}{\overset{{}}{\mathop{\sum }}}\,{i}'\Delta{{t}_{2}}$
联立解得${{q}_{1}}=0.45\;\rm \text{C}$。
高中 | 双棒模型题目答案及解析(完整版)
