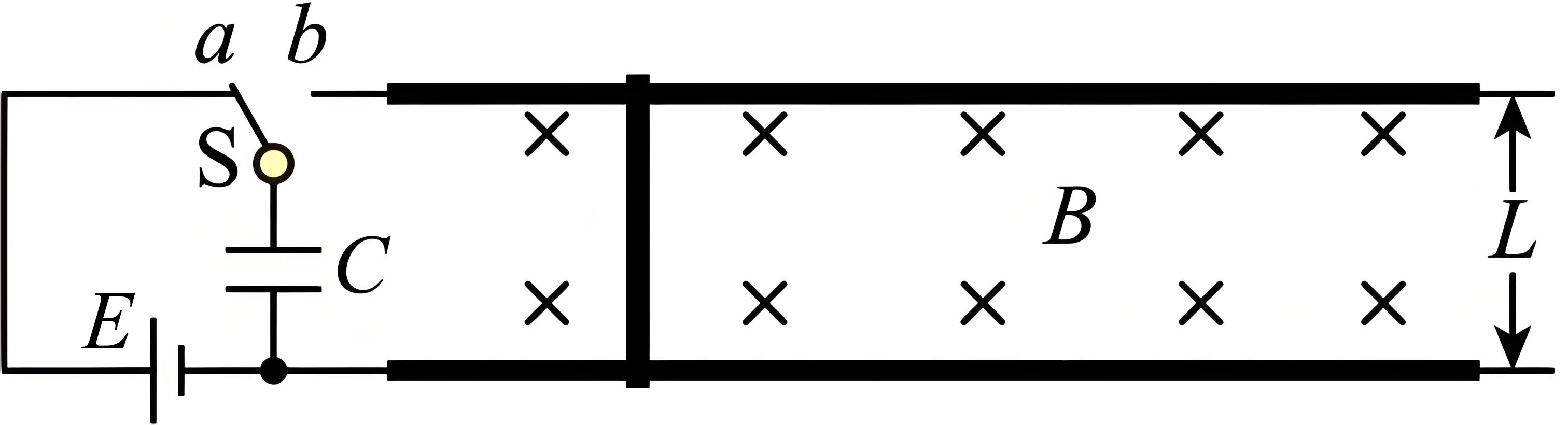
求发射时导体棒能获得的最终发射速度${{v}_{\rm m}}$；

${{v}_{\\text{m}}}=\\dfrac{BLCE}{m+C{{B}^{2}}{{L}^{2}}}$；

导体棒达到最大速度时，感应电动势等于电容器电压$U=BL{{v}_{\text{m}}}$

对导体棒，由动量定理$B\bar{I}Lt=m{{v}_{\text{m}}}$

通过导体棒的电荷量$q=\bar{I}t=C(E-U)$

联立解得${{v}_{\text{m}}}=\dfrac{BLCE}{m+C{{B}^{2}}{{L}^{2}}}$；

已知电容器储存的电场能为$V=\dfrac{1}{2}CU^{2}$，求发射过程中导体棒上产生的焦耳热$Q$；

$Q=\\dfrac{mC{{E}^{2}}}{2m+2C{{B}^{2}}{{L}^{2}}}$；

电容器最终的电压为$U=BL{{v}_{\text{m}}}=\dfrac{{{B}^{2}}{{L}^{2}}CE}{m+C{{B}^{2}}{{L}^{2}}}$

根据能量守恒，导体棒上产生的焦耳热为$Q=\dfrac{1}{2}C{{E}^{2}}-\dfrac{1}{2}C{{U}^{2}}-\dfrac{1}{2}mv_{\text{m}}^{2}$

解得：$Q=\dfrac{mC{{E}^{2}}}{2m+2C{{B}^{2}}{{L}^{2}}}$；

如果磁感应强度$B$的大小可以调节，保持其它参数不变，为使导体棒的最终动能取得最大值，求所加磁感应强度$B$的大小及对应最终发射动能的最大值${{E}_{\text{kmax}}}$。

$B=\\dfrac{1}{L}\\sqrt{\\dfrac{m}{C}}$，${{E}_{\\mathrm{k\\max}}}=\\dfrac{{{E}^{2}}C}{8}$。

根据${{v}_{\text{m}}}=\dfrac{BLCE}{m+C{{B}^{2}}{{L}^{2}}}=\dfrac{LCE}{\dfrac{m}{B}+CB{{L}^{2}}}$

当$\dfrac{m}{B}=CB{{L}^{2}}$时，即$B=\dfrac{1}{L}\sqrt{\dfrac{m}{C}}$时导体棒最终速度达到最大值，最大值为${{v}_{\max}}=\dfrac{E}{2}\sqrt{\dfrac{C}{m}}$

导体棒可获得的最终动能的最大值${{E}_{\text{k}\max}}=\dfrac{1}{2}mv_{\max}^{2}=\dfrac{{{E}^{2}}C}{8}$。