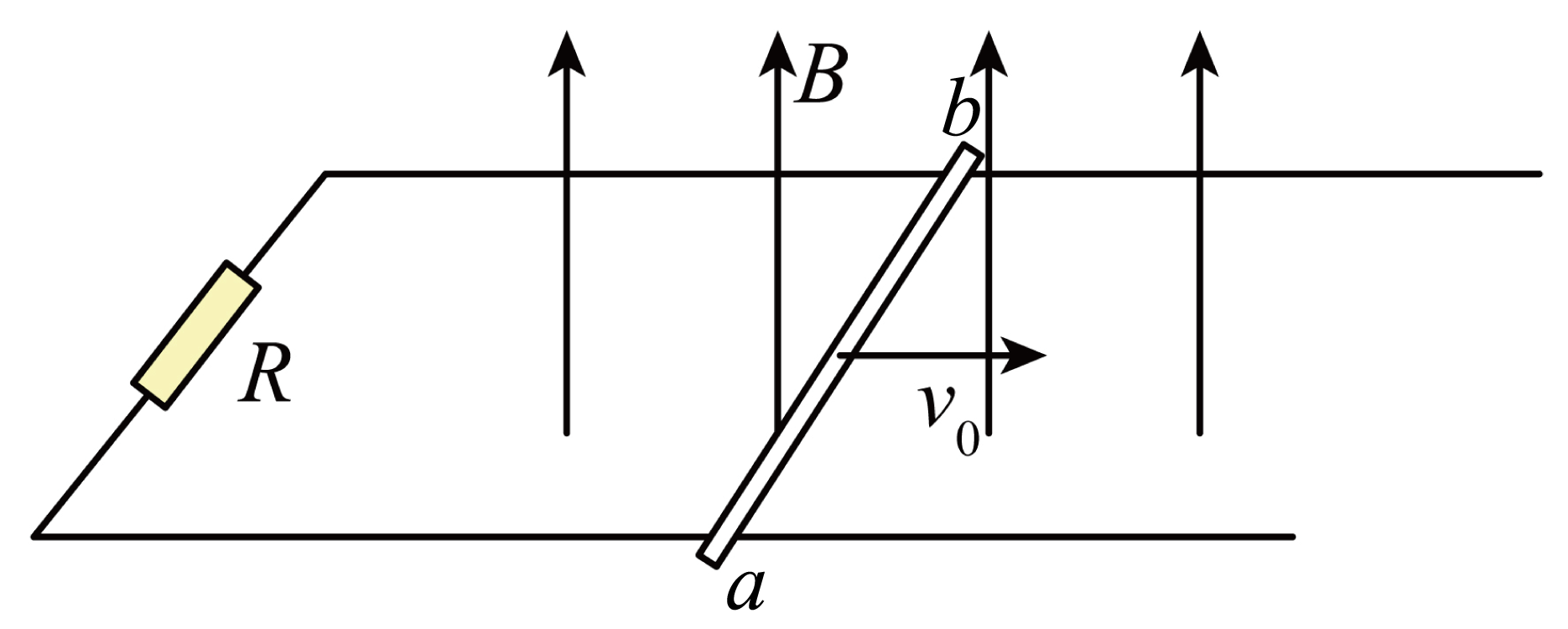
如图所示，绝缘水平面上固定有两根足够长的光滑平行导轨，导轨间距为$d$，左端连接阻值为$R$的定值电阻，一质量为$m$、有效电阻为$r$的导体棒$ab$垂直导轨放置，空间存在竖直向上、磁感应强度大小为$B$的匀强磁场，现给导体棒一个水平向右的初速度$v_{0}$，导体棒在运动过程中始终与导轨接触良好，导轨电阻不计，下列说法正确的是$(\qquad)$

导体棒$a$端的电势较低

导体棒产生的热量为$\\dfrac{mv_{0}^{2}r}{2(R+r)}$

导体棒受到的最大安培力为$\\dfrac{B^{2}d^{2}v_{0}}{R+r}$

导体棒向右运动的最大距离为$\\dfrac{mv_{0}(R+r)}{B^{2}d^{2}}$

$\rm A$．根据右手定则可知，导体棒中的电流由$b$流向$a$，则$a$端电势较高，故$\rm A$错误；

$\rm B$．根据能量守恒定律可知，回路中产生的热量为$Q=\dfrac{1}{2}mv_{0}^{2}$

所以导体棒上产生的热量为$Q_{\text{r}}=\dfrac{r}{R+r}Q=\dfrac{mv_{0}^{2}r}{2(R+r)}$，故$\rm B$正确；

$\rm C$．初始时导体棒受到的安培力最大，即$F=BId=B\dfrac{Bdv_{0}}{R+r}d=\dfrac{B^{2}d^{2}v_{0}}{R+r}$，故$\rm C$正确；

$\rm D$．设导体棒向右运动的最大距离为$x$，则有$- B\overline{I}dt=0-mv_{0}$，$\overline{I}t=\dfrac{Bd\overline{v}}{R+r}t=\dfrac{Bdx}{R+r}$

联立解得$x=\dfrac{mv_{0}(R+r)}{B^{2}d^{2}}$，故$\rm D$正确。

故选：$\rm BCD$。