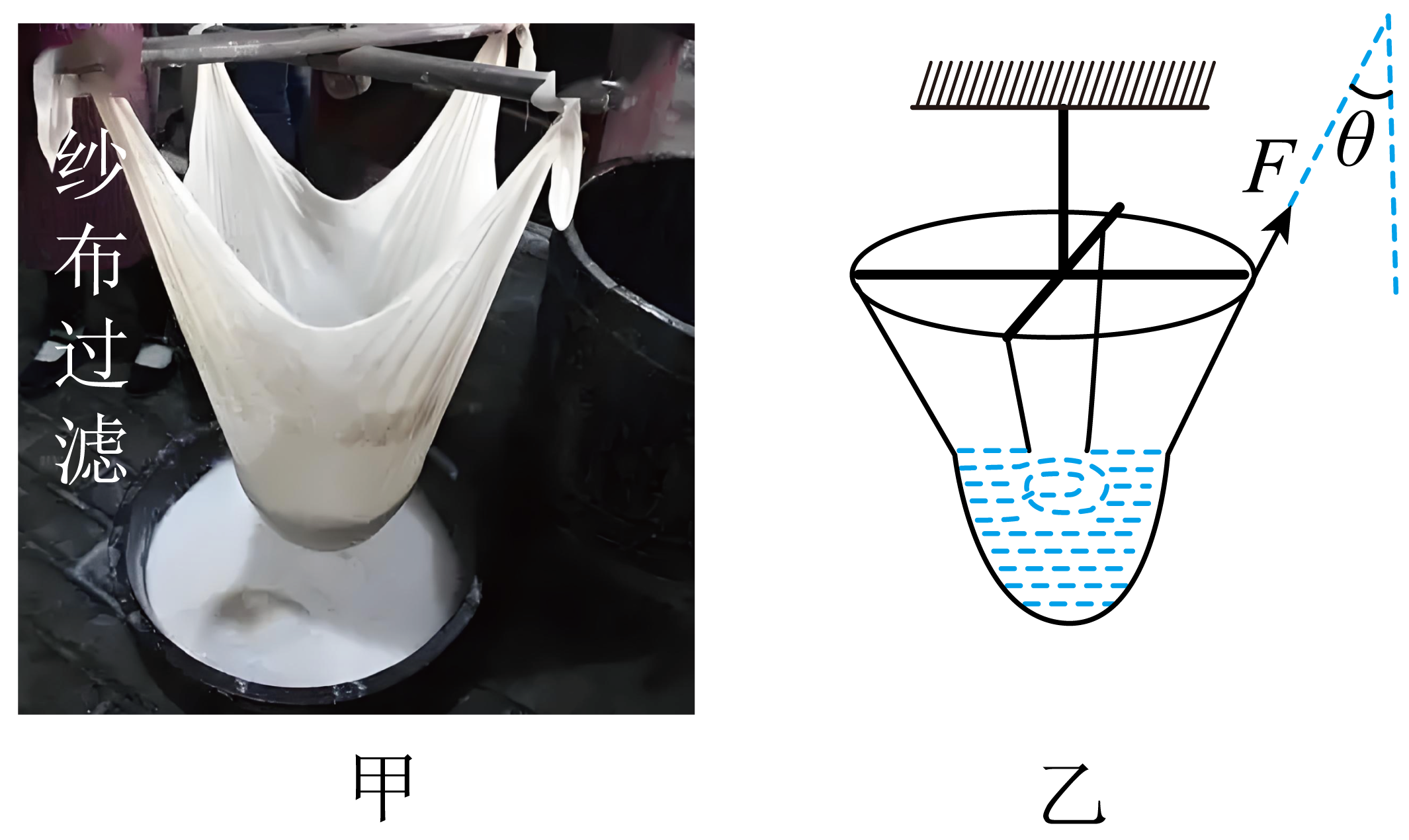
如图甲所示为我国传统豆腐制作流程中的纱布过滤过程，其模型如图乙所示，正方形纱布的四角用细绳系在两根等长的、相互垂直的水平木杆两端，再通过木杆中心转轴静止悬挂在空中。豆浆过滤完，纱布与豆渣的总质量为$m$，细绳与竖直方向的夹角始终为$\theta$，重力加速度为$g$。下列说法正确的是$(\qquad)$

此时每根细绳受到的拉力大小为$\\dfrac{mg}{4\\cos\\theta}$

此时每根细绳受到的拉力大小为$\\dfrac{mg}{4}$

豆浆从纱布流出过程中，忽略纱布的拉伸形变，细绳受到的拉力变大

豆浆从纱布流出过程中，纱布中豆浆和豆渣整体的重心先下降后上升

$\rm AB$$.$以纱布与豆渣为对象，根据受力平衡可得$4F\cos \theta=mg$

可得此时每根细绳受到的拉力大小为$F=\dfrac{mg}{4\cos\theta}$，故$\rm A$正确，$\rm B$错误；

$\rm C$．豆浆流出过程中整体的质量减少，根据$F=\dfrac{mg}{4\cos\theta}$，可知细绳受到的拉力变小，故$\rm C$错误；

$\rm D$．豆浆流出过程中根据整体质量的变化可以判断，豆浆和豆渣整体的重心先向下移，当豆浆流出到一定程度后，豆浆和豆渣整体的重心又会上移，故$\rm D$正确。

故选：$\rm AD$。