高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
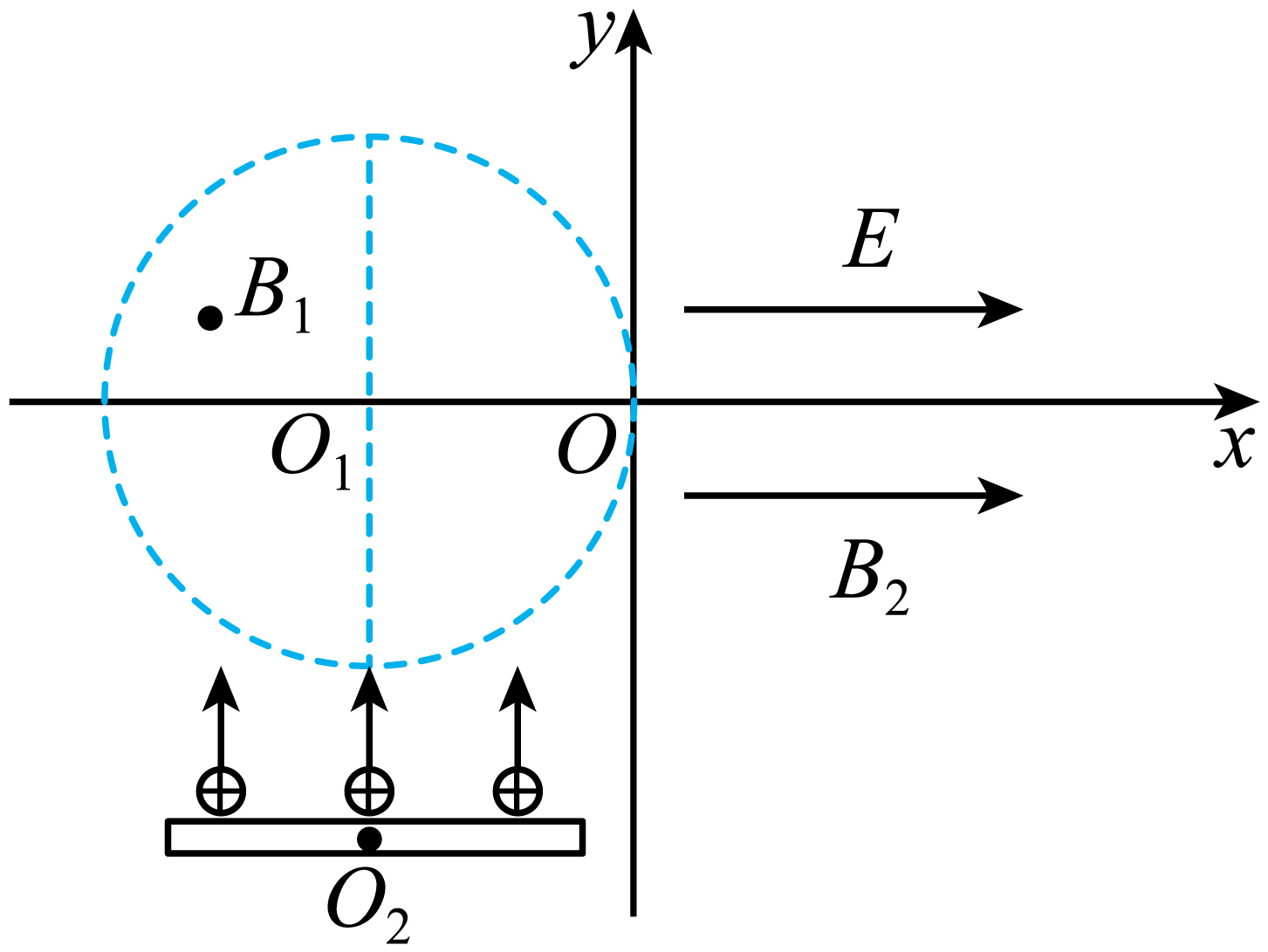
如图所示,空间直角坐标系$Oxyz$($z$轴未画出,正方向向外)中,$xOy$平面内半径为$R$的圆形区域与$y$轴相切于$O$点,圆心在$O_{1}$处,区域内的匀强磁场沿$z$轴正方向,磁感应强度为$B_{1}$,$x \gt 0$区域内,匀强电场和匀强磁场的方向均沿$x$轴正方向,电场强度为$E$,磁感应强度为$B_{2}$。$xOy$平面的第三象限内有一平行于$x$轴的线状粒子发射器,中点在$O_{2}$处,$O_{1}$与$O_{2}$的连线平行于$y$轴,粒子发射器可在宽度为$1.6R$的范围内沿$y$轴正方向发射质量为$m$,电荷量为$q(q \gt 0)$的同种粒子,发射速度大小可调,$\sin 53^\circ =0.8$,$\cos 53^\circ =0.6$。
若从$O_{2}$点发出的粒子,飞出磁场时速度偏转了$60^\circ $角,求该粒子的速度大小$v_{1}$;
$\\dfrac{\\sqrt{3}qB_{1}R}{m}$;
"]]粒子运动轨迹如图甲所示,设轨迹半径为$r_{1}$
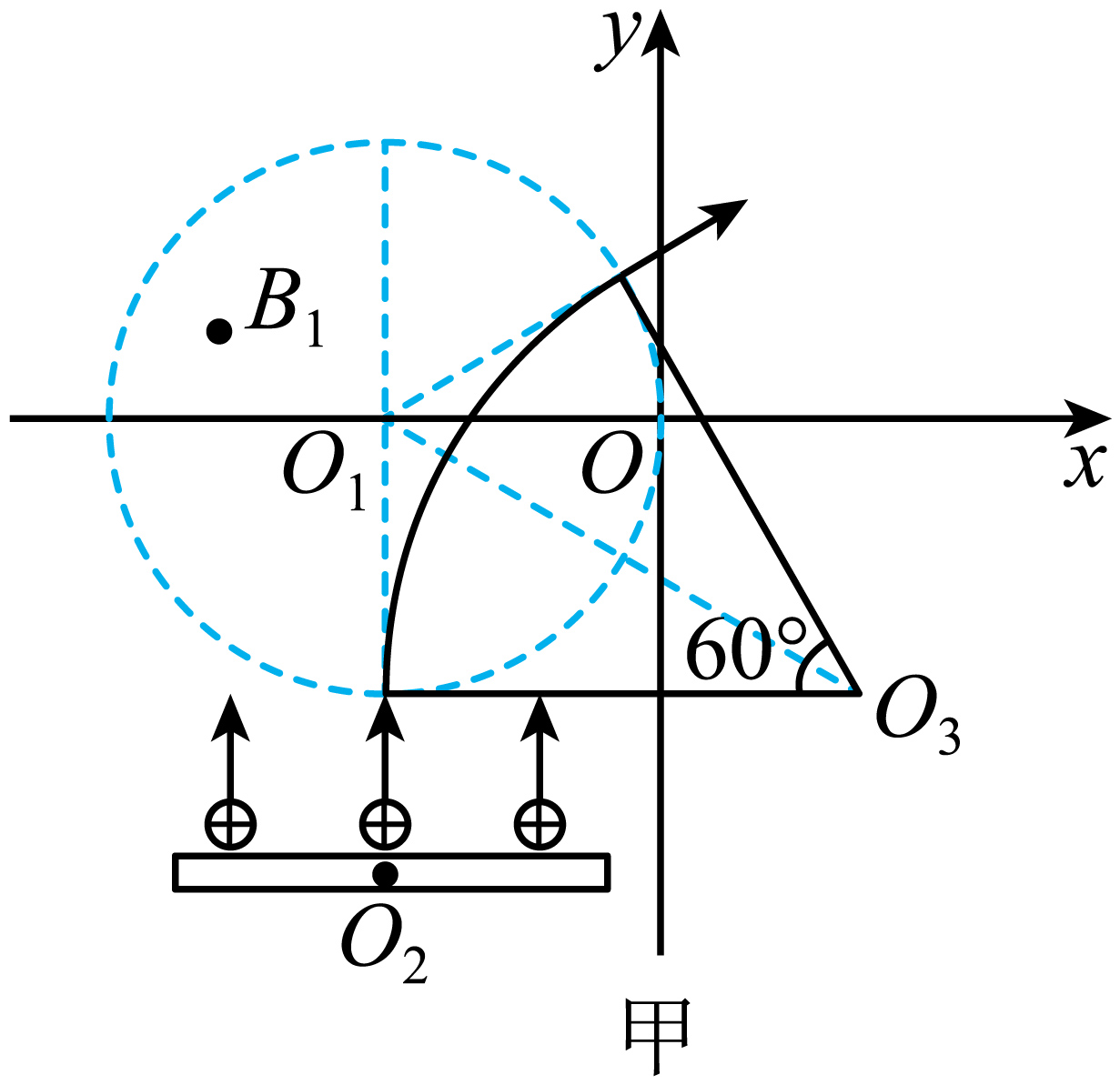
由几何关系得:$r_{1} ⋅ \tan 30^\circ =R$
洛伦兹力充当向心力:$qv_{1}B_{1}=m\dfrac{v_{1}^{2}}{r_{1}}$
解得$:v_{1}=\dfrac{\sqrt{3}qB_{1}R}{m}$;
若粒子的发射速度大小$v_{2}= \dfrac{\sqrt{2}qB_{1}R}{m}$,求在磁场中运动时间最长的粒子进入圆形磁场时的位置到$O_{1}O_{2}$的距离;
$\\dfrac{\\sqrt{2}}{2}R$;
"]]由$qv_{2}B_{1}= m\dfrac{v_{2}^{2}}{r_{2}}$
得:$r_{2}=\sqrt{2}R$
设从$C$点进,$D$点出的粒子在磁场中运动时间最长,则$CD$为圆形磁场的直径
粒子运动轨迹如图乙所示,$∠CO_{4}D=90^\circ $,由几何关系得:$r_{2} ⋅ \sin\alpha=R$
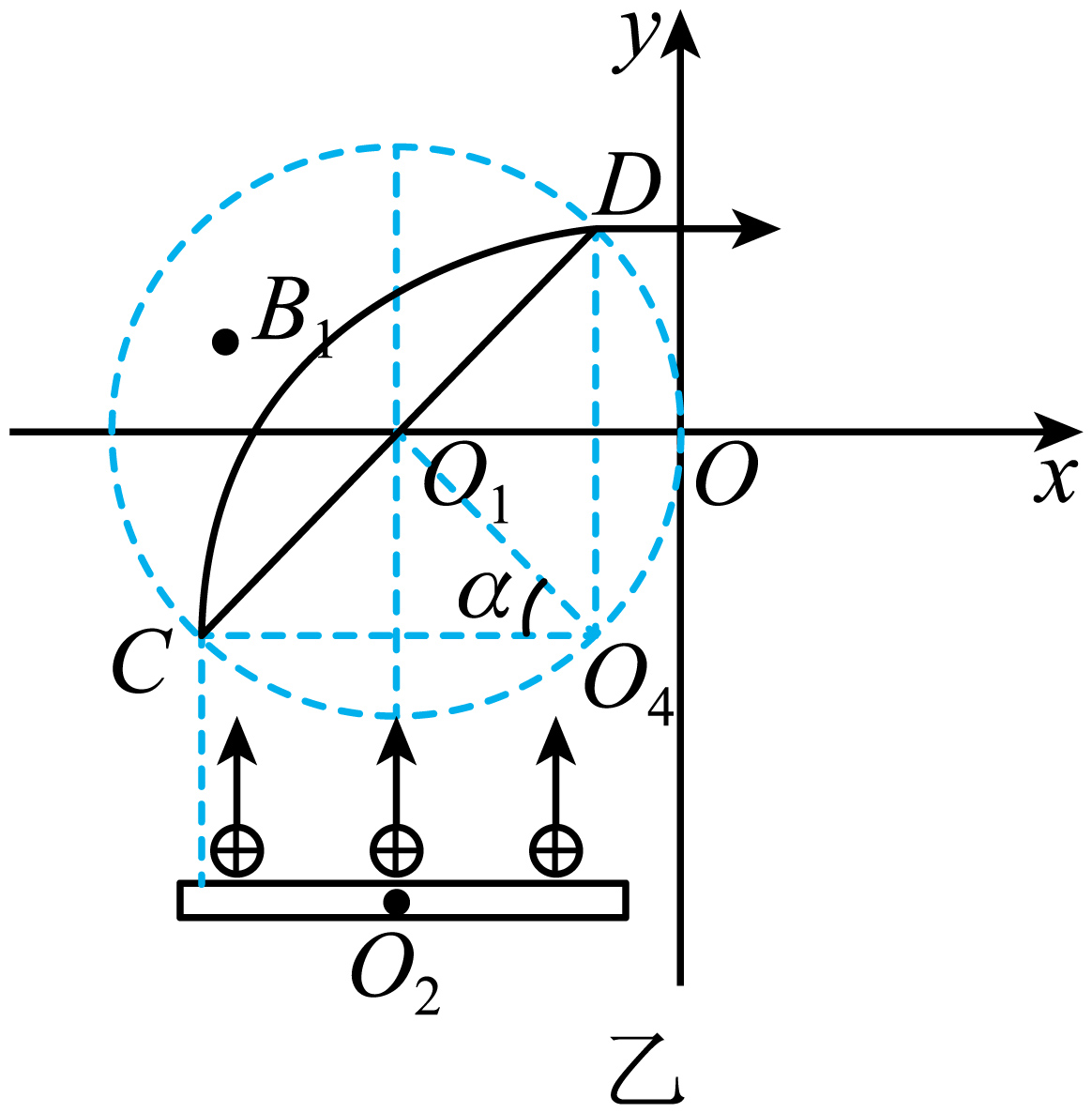
解得:$\sin\alpha=\dfrac{\sqrt{2}}{2}$
由几何关系得:该粒子的入射位置到$O_{1}O_{2}$的距离$d=R \cdot \sin\alpha=\dfrac{\sqrt{2}}{2}R$;
调整粒子发射速度的大小为某一值时,所有粒子均从$O$点飞出圆形磁场。求从发射器最左端发射的粒子进入$x \gt 0$区域后,运动轨迹上与$x$轴距离最远点的位置坐标。
$\\left( \\dfrac{3(2n+1)\\pi B_{1}R}{5B_{2}}+\\dfrac{\\pi^{2}mE{(2n+ 1)}^{2}}{2qB_{2}^{2}},0,\\dfrac{8B_{1}R}{5B_{2}} \\right)(n= 0,1,2\\cdots\\cdots)$。
"]]由题意得:粒子在圆形磁场中的运动半径$r_{3}=R$
由$qv_{3}B_{1}=m\dfrac{v_{3}^{2}}{r_{3}}$
得:$v_{3}=\dfrac{qB_{1}R}{m}$
发射器最左端发射的粒子运动轨迹如图丙所示,设该粒子运动到$O$点时其速度方向与$x$轴正方向夹角为$\beta$
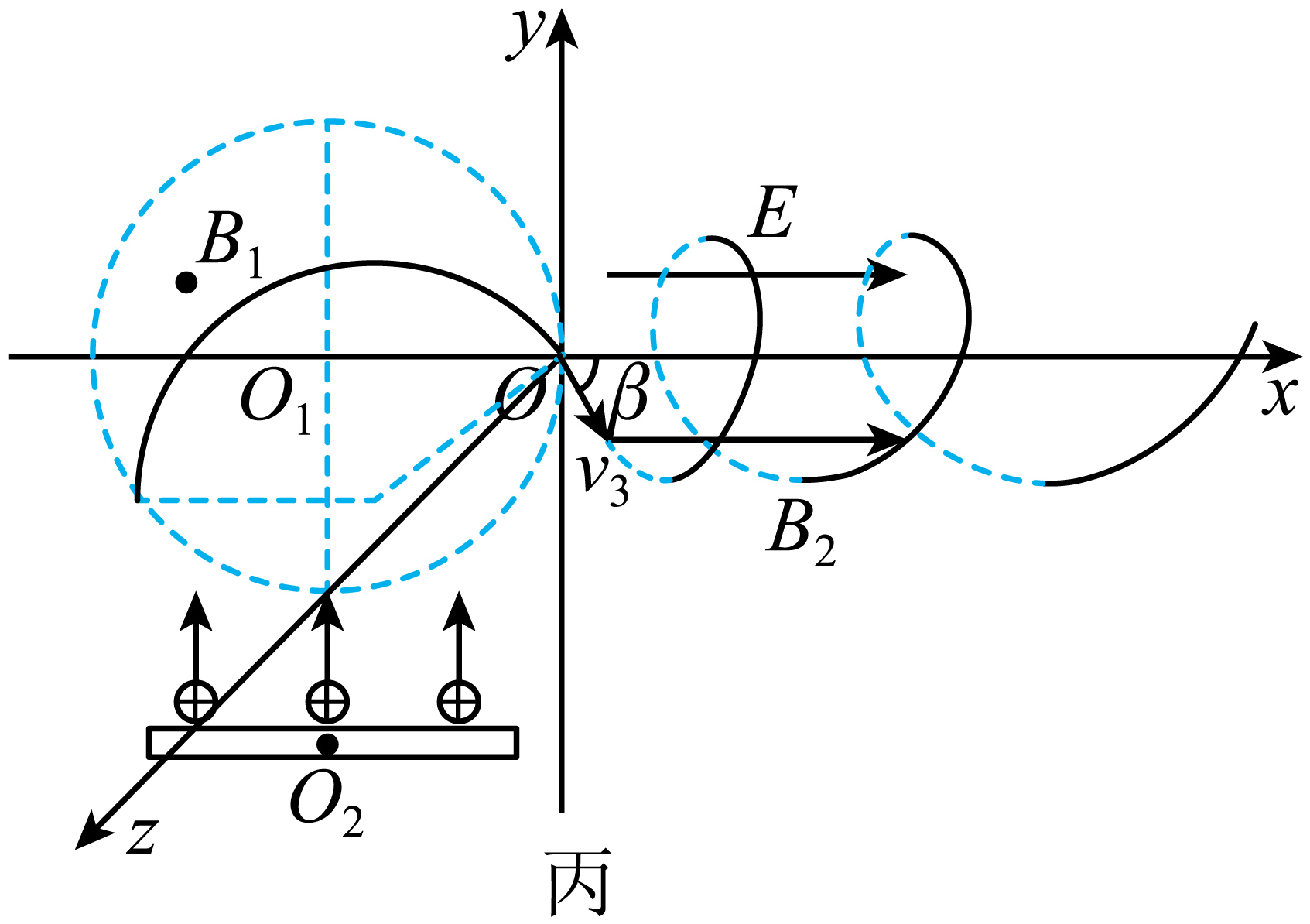
由几何关系$r_{3}+r_{3}\sin\beta=1.8R$
得$\sin\beta=0.8$,$v_{x}=v_{3} ⋅ \cos\beta$,$v_{y}=v_{3} ⋅ \sin\beta$
由题意得:该粒子的运动可视为沿$x$轴正方向的匀加速直线运动和垂直于$x$轴平面内的匀速圆周运动的合运动$a=\dfrac{qe}{m}$,$qv_{y}B_{2}=m\dfrac{v_{y}^{2}}{r_{4}}$
解得$r_{4}=\dfrac{4B_{1}R}{5B_{2}}$
粒子轨迹上的点与$x$轴的最远距离为$2r_{4}=\dfrac{8B_{1}R}{5B_{2}}$,$T=\dfrac{2\pi r_{4}}{v_{y}}=\dfrac{2\pi m}{qB_{2}}$
则粒子从经过$O$点开始运动到距离$x$轴最远处的时间为$t=\dfrac{T}{2}+nT=(2n+1)\dfrac{\pi m}{qB_{2}}(n=0,1,2\cdots\cdots)$
由$x=v_{x}t+\dfrac{1}{2}at^{2}$
得$x=\dfrac{3(2n+1)\pi B_{1}R}{5B_{2}}+\dfrac{\pi^{2}mE{(2n+1)}^{2}}{2qB_{2}^{2}}(n=0,,2\cdots\cdots)$
即粒子运动轨迹上与$x$轴距离最远的位置坐标为$\left( \dfrac{3(2n+1)\pi B_{1}R}{5B_{2}}+\dfrac{\pi^{2}mE{(2n+1)}^{2}}{2qB_{2}^{2}},0,\dfrac{8B_{1}R}{5B_{2}} \right)(n=0,1,2\cdots\cdots)$。
高中 | 洛伦兹力题目答案及解析(完整版)
