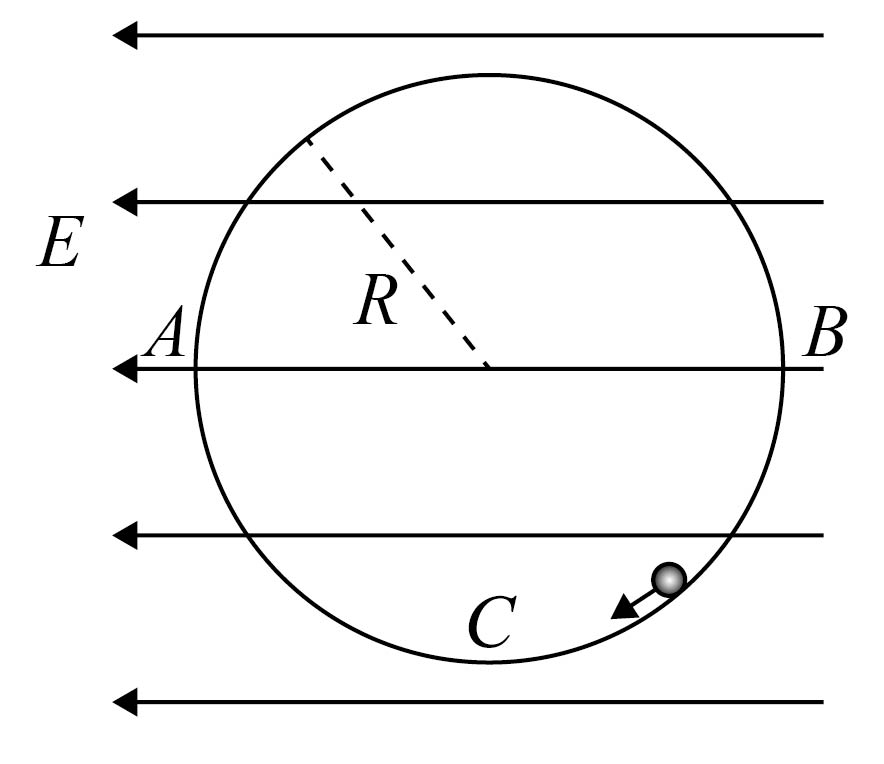
带电小球在$B$点速度大小；

$3\\sqrt{gR}$

由题意得：$N=11mg$，$Eq=2mg$，对$B$点受力分析可得$N-Eq=m\dfrac{v_{B}^{2}}{R}$

解得${{v}_{B}}=3\sqrt{gR}$

带电小球在$C$点时对轨道压力大小；

$8mg$

从$C$点到$B$点，由动能定理得：$EqR-mgR=\dfrac{1}{2}mv_{B}^{2}-\dfrac{1}{2}mv_{C}^{2}$，可得${{v}_{C}}=\sqrt{7gR}$

小球在$C$点时，对其受力分析，由牛顿第二定律得${{N}_{2}}-mg=m\dfrac{v_{C}^{2}}{R}$，解得${{N}_{2}}=8mg$

根据牛顿第三定律可知，小球在$C$点时对轨道压力大小$8$$mg$。

此过程中带电小球在圆轨道上运动的最小动能。

$\\left( \\dfrac{5}{2}-\\sqrt{5} \\right)mgR$

小球能在竖直面内做完整的圆周运动，在等效最高点$D$点（如图所示）时速度最小，在$D$点重力和电场力的合力方向指向圆心，此时$D$点与圆心的连线与竖直方向的夹角为$\text{ }\!\!\theta\!\!\text{ }$，则有$\text{tan}\theta =\dfrac{Eq}{mg}=2$

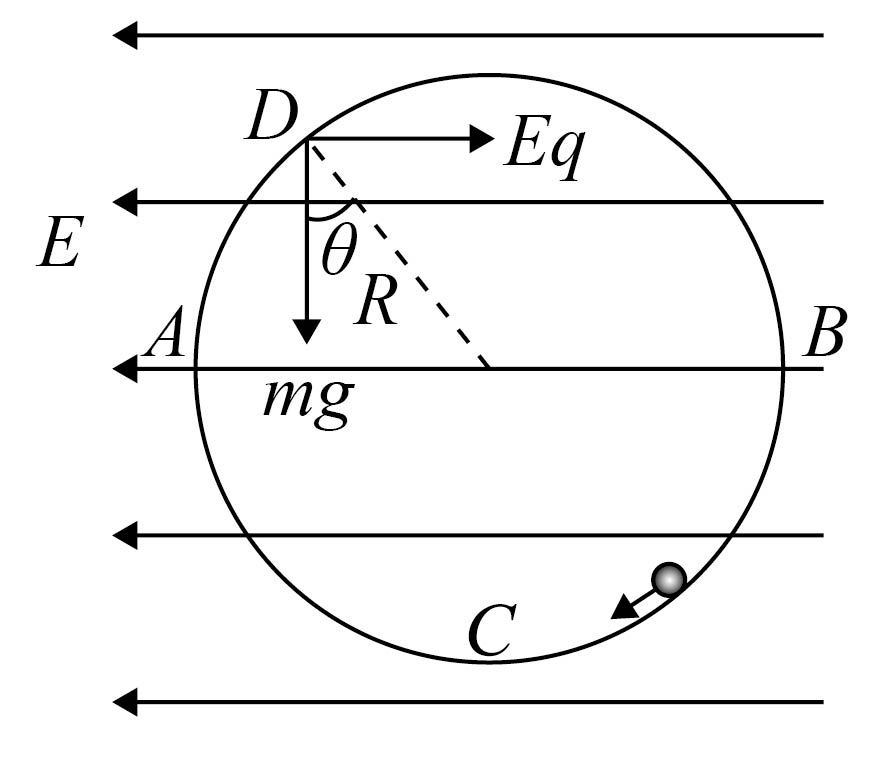
小球从$C→$$D$由动能定理得：$-mgR\cdot \left( 1+\dfrac{1}{\sqrt{5}} \right)-EqR\cdot \dfrac{2}{\sqrt{5}}=\dfrac{1}{2}mv_{D}^{2}-\dfrac{1}{2}mv_{C}^{2}$

带电小球在圆轨道上运动的最小动能${{E}_{kD}}=\left( \dfrac{5}{2}-\sqrt{5} \right)mgR$