如图所示，回旋加速器$\rm D$形盒的半径为$R$，所加磁场的磁感应强度大小为$B$、方向垂直$\rm D$形盒向下。质子从$\rm D$形盒中央由静止出发，经电压为$U$的交变电场加速后进入磁场，若质子的质量为$m$，带电荷量为$e$，质子在电场中运动的时间忽略不计，则下列分析正确的是$(\qquad)$

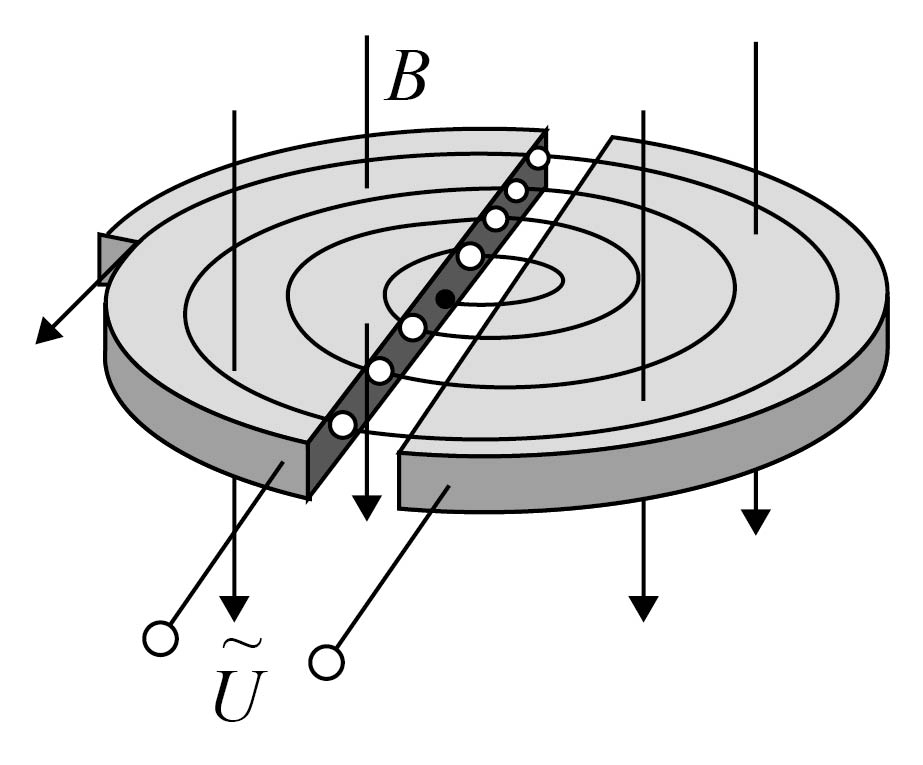
质子在回旋加速器中加速后获得的最大动能为$\\dfrac{e^{2}B^{2}R^{2}}{2m}$

质子在回旋加速器中加速的次数为$\\dfrac{\\pi m}{eB}$

质子在回旋加速器中加速的次数为$\\dfrac{2eB^{2}R^{2}}{mU}$

质子在回旋加速器中运动的时间为$\\dfrac{\\pi BR^{2}}{2U}$

$\rm A$．质子在磁场中做匀速圆周运动，质子轨道半径等于$\rm D$型盒半径$R$时速度最大，对质子，由牛顿第二定律得$evB=m\dfrac{v^{2}}{R}$，质子的最大动能$E_{\rm km}=\dfrac{1}{2}mv^{2}$，解得$E_{\rm km}=\dfrac{e^{2}B^{2}R^{2}}{2m}$，故$\rm A$正确；

$\rm BC$．对质子，由动能定理得$neU=\dfrac{1}{2}mv^{2}-0$，解得$n=\dfrac{eB^{2}R^{2}}{2mU}$，故$\rm BC$错误；

$\rm D$．质子在磁场中做匀速圆周运动的周期$T=\dfrac{2\pi r}{v}=\dfrac{2\pi m}{eB}$，质子在回旋加速器中的运动时间$t=\dfrac{n}{2}T$，解得$t=\dfrac{\pi BR^{2}}{2U}$，故$\rm D$正确。

故选：$\rm AD$。