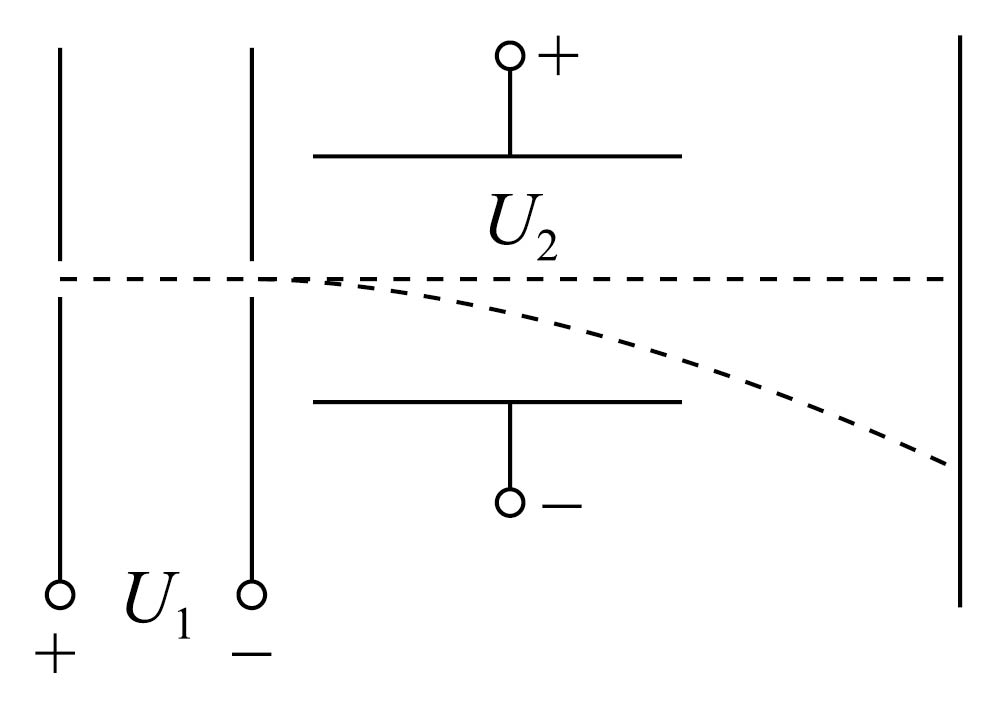
如图所示，有两种比荷不同的带正电的粒子，其中带电粒子$\rm A$的比荷大于带电粒子$\rm B$的比荷，$\rm A$、$\rm B$两种粒子先后进入加速电场加速，然后进入偏转电场，最后打在偏转电场右侧的屏上，带电粒子进入电场加速时的初速度忽略不计，不考虑重力的影响，下列说法正确的是$(\quad\ \ \ \ )$

离开加速电场时，$\\rm A$的速度比$\\rm B$的速度大

离开偏转电场时，$\\rm A$、$\\rm B$的偏转距离相等

偏转电场对$\\rm A$、$\\rm B$所做的功一定相等

从进入加速电场到离开偏转电场，$\\rm A$、$\\rm B$的运动时间相等

$\rm A$．粒子在加速电场中，根据动能定理有$q{{U}_{1}}=\dfrac{1}{2}m{{v}_{0}}^{2}$，解得${{v}_{0}}=\sqrt{\dfrac{2q{{U}_{1}}}{m}}$，带电粒子$\rm A$的比荷大于带电粒子$\rm B$的比荷，则离开加速电场时，$\rm A$的速度比$\rm B$的速度大，故$\rm A$正确；

$\rm B$．粒子在偏转电场中做类平抛运动，设板长为$L$，间距为$d$，则$L={{v}_{0}}t$，$y=\dfrac{1}{2}a{{t}^{2}}$；

根据牛顿第二定律有$a=\dfrac{q{{U}_{2}}}{md}$，解得$y=\dfrac{{{U}_{2}}{{L}^{2}}}{4{{U}_{1}}d}$，则离开偏转电场时，$\rm A$、$\rm B$的偏转距离相等，故$\rm B$正确；

$\rm C$．偏转电场中，电场力做功为$W=qEy=\dfrac{q{{U}_{2}}^{2}{{L}^{2}}}{4{{U}_{1}}{{d}^{2}}}$，由于电量关系未知，故无法判断电场做功大小关系，故$\rm C$错误；

$\rm D$．设加速电场的宽度为${d}'$，在加速电场中由动量定理有：$\dfrac{q{{U}_{1}}}{{{d}'}}{t}'=m{{v}_{0}}$

从进入加速电场到离开偏转电场，运动时间为${t}''=t+{t}'$，解得${t}''=\left( 2{d}'+L \right)\sqrt{\dfrac{m}{2q{{U}_{1}}}}$，则从进入加速电场到离开偏转电场，$\rm A$的运动时间小于$\rm B$的运动时间，故$\rm D$错误；

故选$\rm AB$。