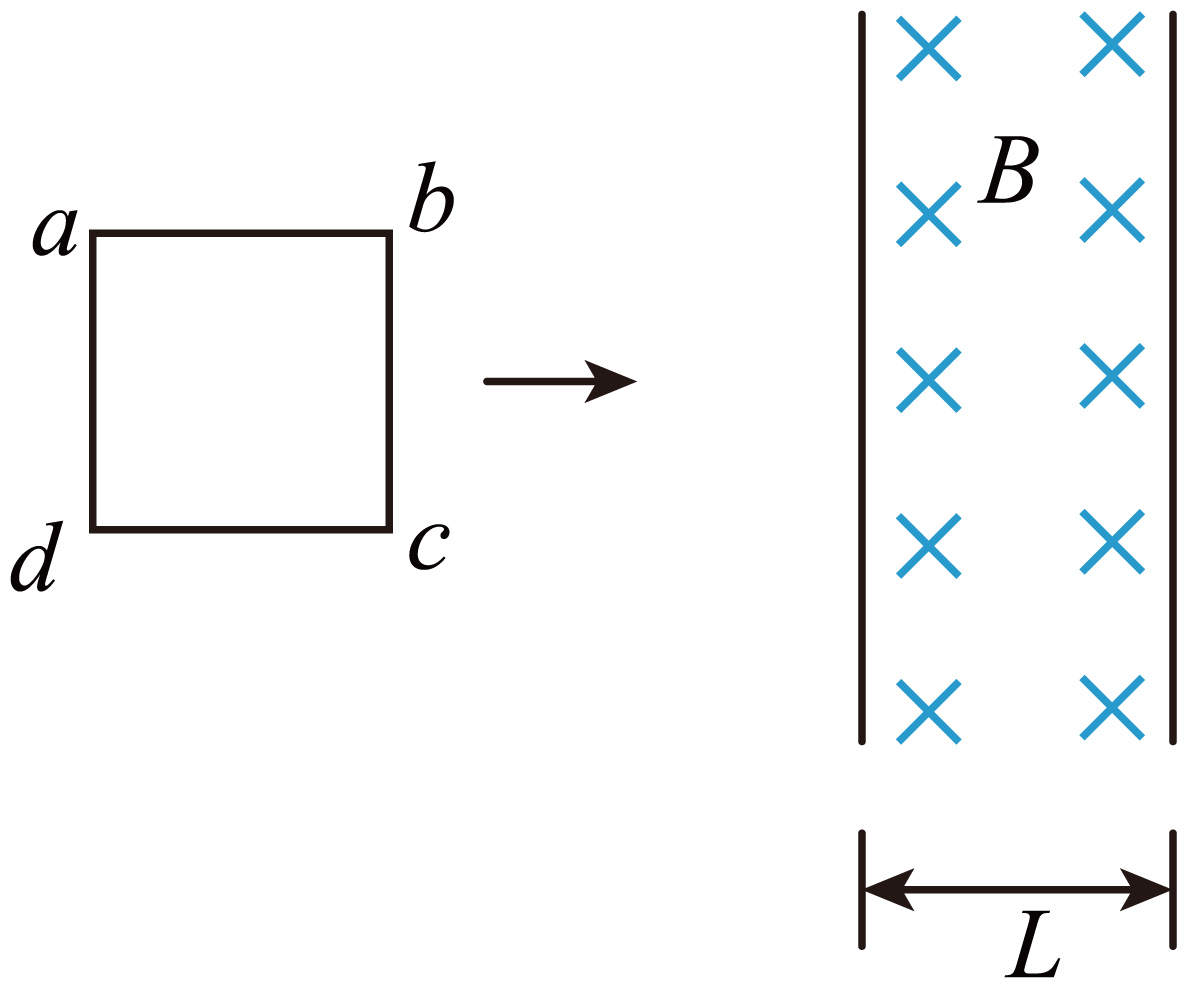
某学习小组研究线框通过磁场时产生的阻尼与线框形状等因素的关系。光滑绝缘水平面上宽度为$L$的区域内存在竖直向下的匀强磁场，磁感应强度为$B$，一周长为$4L$的线框$abcd$，质量为$m$。①如图所示，线框为正方形时，初速度为$v_{0}$，$bc$边平行磁场边界进入磁场，线框离开磁场时的速度是进入磁场时的一半。②线框为矩形，初速度不变，左、右边长为$\dfrac{4}{3}L$。下列说法正确的是$(\qquad)$

①情况下线框进入磁场过程安培力的冲量大小为$\\dfrac{3}{4}mv_{0}$

①情况下线框穿出磁场过程产生的电热为$\\dfrac{5}{32}mv_{0}^{2}$

②情况下线框穿出磁场的速度大小为$\\dfrac{11}{27}v_{0}$

②情况下整个过程线框产生的电热为$\\dfrac{4}{9}mv_{0}^{2}$

设线框电阻为$R$，$bc$边长为$L_{1}$，$ab$边长为$L_{2}(L_{2} \leqslant L)$，线框完全进入磁场时速度为$v_{t1}$，线框进入磁场过程中，设某一时刻的速度为$v$，感应电动势$E=BL_{1}v$

感应电流$I=\dfrac{E}{R}=\dfrac{BL_{1}v}{R}$

安培力$F=BIL_{1}=\dfrac{B^{2}L_{1}^{2}v}{R}$

经过一小段时间$\Delta t(\Delta t → 0)$，由动量定理，有$−F\Delta t=m\Delta v$

得$- \dfrac{B^{2}L_{1}^{2}v}{R} \times \Delta t=m\Delta v$

线框前进位移$\Delta x=v\Delta t$

求和有$- \dfrac{B^{2}L_{1}^{2}L_{2}}{R}=m\left( v_{t1}-v_{0} \right)$

同理出磁场过程有$- \dfrac{B^{2}L_{1}^{2}L_{2}}{R}=m\left( v_{末}-v_{t1} \right)$

$\rm AB$．①情况下，可得线框完全进入磁场时的速度$v_{t1}=\dfrac{3}{4}v_{0}$

则线框进入磁场过程安培力的冲量大小为$mv_{0}-mv_{t1}=\dfrac{1}{4}mv_{0}$

穿出磁场过程产生的电热为$Q_{电1}=\dfrac{1}{2}mv_{t1}^{2}-\dfrac{1}{2}m\left( \dfrac{v_{0}}{2} \right)^{2}$

解得$Q_{电1}=\dfrac{5}{32}mv_{0}^{2}$，$\rm A$错误，$\rm B$正确；

$\rm CD$．②情况下，线框穿出磁场的速度大小为${v'}_{末}=\dfrac{11}{27}v_{0}$

整个过程线框产生的电热为$Q_{电2}=\dfrac{1}{2}mv_{0}^{2}-\dfrac{1}{2}m\left( \dfrac{11v_{0}}{27} \right)^{2}=\dfrac{304}{729}mv_{0}^{2}$，$\rm C$正确，$\rm D$错误。

故选：$\rm BC$。