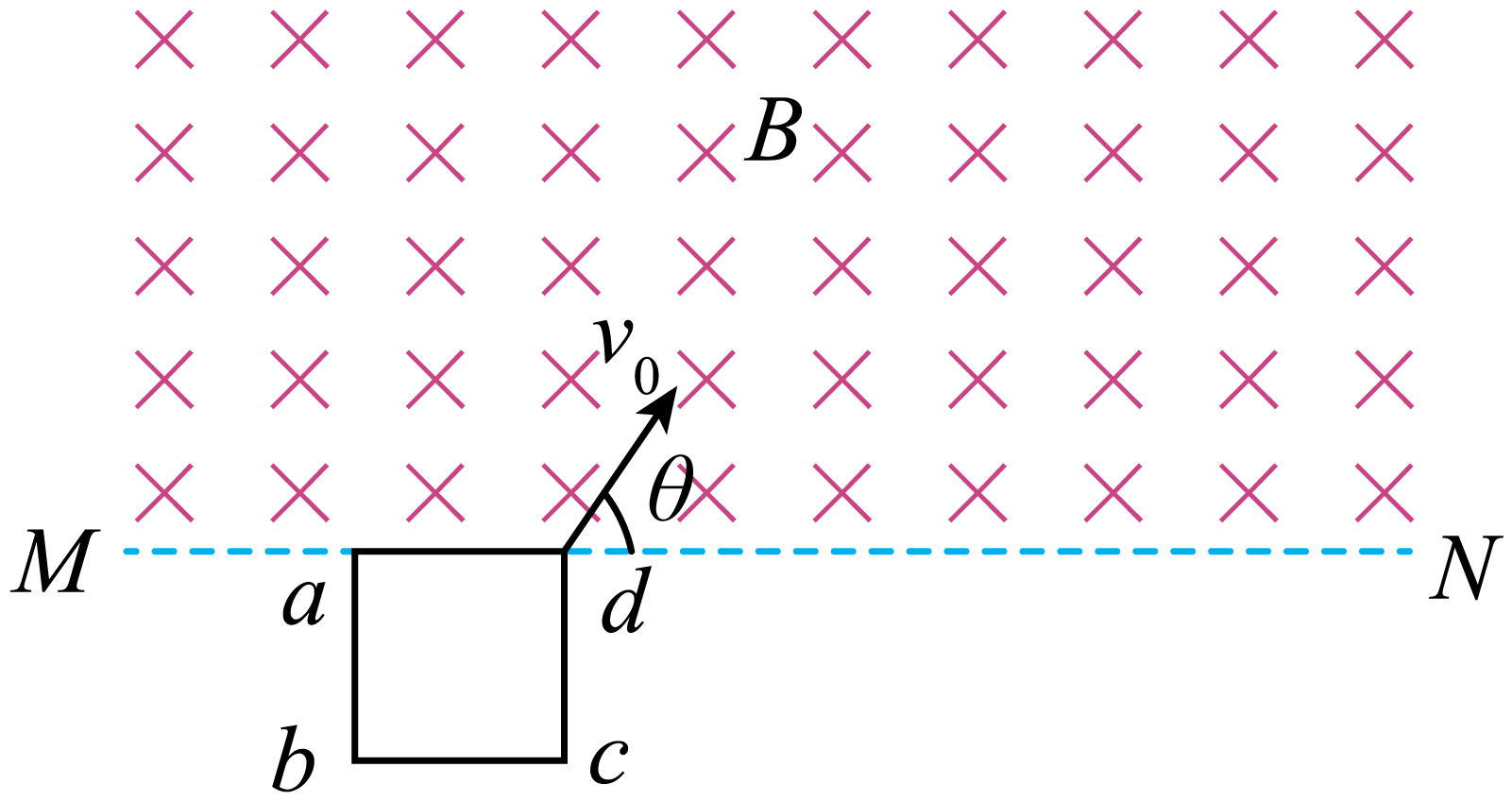
如图所示，边长$L=0.4\;\rm m$、质量$m=0.2\;\rm kg$、电阻$R=0.1\;\rm \Omega$的正方形线框$abcd$置于光滑水平桌面上，$ad$边与匀强磁场边界$MN$重合。$t=0$时刻，线框以初速度$v_{0}$进入磁感应强度方向竖直向下的匀强磁场中，$v_{0}$方向与磁场边界$MN$的夹角$\theta=53^\circ$，线框恰好能够全部进入匀强磁场。已知匀强磁场的磁感应强度大小为$1.0\;\rm T$，$\sin 53^\circ =0.8$，$\cos 53^\circ =0.6$，线框进入磁场的过程中，$ad$边始终与磁场边界平行，则下列说法正确的是$(\qquad)$

线框的初速度大小$v_{0}=4\\;\\rm m/s$

线框进入磁场过程中最大的加速度大小为$20\\;\\rm m/s^{2}$

线框进入磁场的过程中，通过线框导线横截面的电荷量为$0.8\\;\\rm C$

线框进入磁场过程中产生的焦耳热为$1.024\\;\\rm J$

$\rm A$．线框恰好能够全部进入匀强磁场，表明线框最终沿边界做匀速直线运动，根据动量定理有$- B\overline{I}L\Delta t=0-mv_{0}\sin\theta$

根据闭合电路欧姆定律有$\overline{I}=\dfrac{BL\overline{v_{y}}}{R}$

其中$L=\overline{v_{y}}\Delta t$

解得$v_{0}=4\;\rm m/s$，$\rm A$项正确；

$\rm B$．线框刚进入磁场时，感应电动势最大，感应电流最大，则有$I_{\max}=\dfrac{BLv_{0}\sin\theta}{R}$，$a_{\max}=\dfrac{BI_{\max}L}{m}$

解得$a_{\max}=25.6\;\rm m/s^{2}$，$\rm B$项错误；

$\rm C$．结合上述，$q=\overline{I}\Delta t$

解得$q=1.6\;\rm C$，$\rm C$项错误；

$\rm D$．根据能量守恒定律有$Q=\dfrac{1}{2}m{v_{0}}^{2}-\dfrac{1}{2}m{(v_{0}\cos\theta)}^{2}=\dfrac{1}{2}m{(v_{0}\sin\theta)}^{2}=1.024\;\rm \text{J}$，$\rm D$项正确。

故选：$\rm AD$。