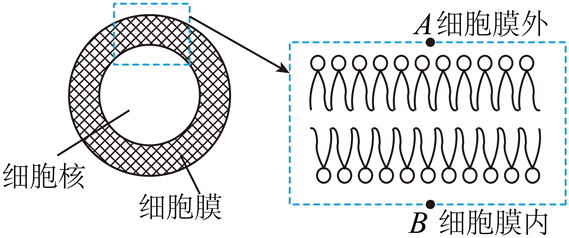
如图所示，人体的细胞膜由磷脂双分子层组成，双分子层之间存在电压（医学上称为膜电位），使得只有带特定电荷的粒子才能通过细胞膜进入细胞内。初速度为${{v}_{0}}$的正一价钠离子仅在电场力的作用下，从细胞膜外$A$点刚好运动到细胞膜内$B$点。将膜内的电场看作匀强电场，已知$A$点电势为${{\varphi }_{a}}$，正一价钠离子质量为$m$，质子电荷量为$e$，细胞膜的厚度为$d$。下列说法正确的是$(\quad\ \ \ \ )$

钠离子匀减速直线运动的加速度大小$a=\\dfrac{v_{0}^{2}}{d}$

膜内匀强电场的场强$E=\\dfrac{mv_{0}^{2}}{ed}$

$B$点电势${{\\varphi }_{b}}={{\\varphi }_{a}}+\\dfrac{mv_{0}^{2}}{e}$

钠离子在$B$点的电势能为${{E}_{b}}={{\\varphi }_{a}}e+\\dfrac{mv_{0}^{2}}{2}$

$\rm A$．正一价钠离子做匀减速直线运动，刚好到达$B$点，即到达$B$点时速度为零，由$0-v_{0}^{2}=$$-2$$ad$，解得加速度大小$a=\dfrac{v_{0}^{2}}{2d}$，故$\text{A}$错误；

$\rm B$．由牛顿第二定律可知$Ee=ma$，解得$E=\dfrac{mv_{0}^{2}}{2ed}$，故$\text{B}$错误；

$\rm C$．由动能定理可得$\left( {{\varphi }_{a}}-{{\varphi }_{b}} \right)e=0-\dfrac{1}{2}mv_{0}^{2}$，解得$B$点电势为${{\varphi }_{b}}={{\varphi }_{a}}+\dfrac{mv_{0}^{2}}{2e}$，故$\text{C}$错误；

$\rm D$．钠离子在$B$点电势能为${{E}_{b}}={{\varphi }_{b}}e={{\varphi }_{a}}e+\dfrac{mv_{0}^{2}}{2}$，故$\rm D$正确。

故选$\rm D$。