高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
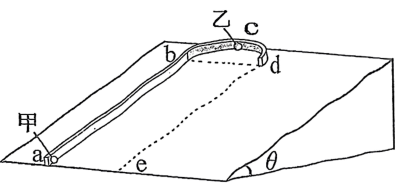
如图所示,倾角为$\theta$的斜面固定于水平地面,斜面上固定有半径为$R$的半圆挡板和长为$7R$的直挡板。$a$为直挡板下端点,$bd$为半圆挡板直径且沿水平方向,$c$为半圆挡板最高点,两挡板相切于$b$点,$de$与$ab$平行且等长。小球乙被锁定在$c$点。小球甲从$a$点以一定初速度出发,沿挡板运动到$c$点与小球乙发生完全弹性碰撞,碰撞前瞬间解除对小球乙的锁定,小球乙在此后的运动过程中无其他碰撞。小球甲质量为$m_{1}$,两小球均可视为质点,不计一切摩擦,重力加速度大小为$g$。
求小球甲从$a$点沿直线运动到$b$点过程中的加速度大小;
$g\\sin \\theta$;
"]]小球甲从$a$点沿直线运动到$b$点过程中,根据牛顿第二定律有$m_{1}g\sin \theta=m_{1}a_{1}$
解得甲在$ab$段运动的加速度大小$a_{1}=g\sin \theta$;
若小球甲恰能到达$c$点,且碰撞后小球乙能运动到$e$点,求小球乙与小球甲的质量比值应满足的条件;
$\\dfrac{m_{1}}{m_{2}} \\geqslant 1$或$\\dfrac{m_{1}}{m_{2}}= \\dfrac{1}{7}$;
"]]甲恰能到$c$点,设到达$c$点时的速度为$v_{1}$,可知$m_{1}g\sin\theta= m_{1}\dfrac{{v_{1}}^{2}}{R}$
解得$v_{1}=\sqrt{gR\sin\theta}$①
根据题意甲乙发生完全弹性碰撞,碰撞前后根据动量守恒和能量守恒$m_{1}v_{1}=m_{1}v_{1}'+m_{2}v_{2}$,$\dfrac{1}{2}m_{1}{v_{1}}^{2}=\dfrac{1}{2}m_{1}{v_{1'}}^{2}+\dfrac{1}{2}m_{2}{v_{2}}^{2}$
解得碰后乙的速度为$v_{2}=\dfrac{2m_{1}v_{1}}{m_{1}+m_{2}}$②
碰后乙能运动至$e$点,第一种情况,碰后乙顺着挡板做圆周运动后沿着斜面到达$e$点,此时需满足$m_{2}g\sin\theta \leqslant m_{2}\dfrac{{v_{2}}^{2}}{R}$
即$v_{2} \geqslant \sqrt{gR\sin\theta}$③
联立①②③可得$\dfrac{m_{1}}{m_{2}} \geqslant 1$
第二种情况,碰后乙做类平抛运动到达$e$点,此时可知$7R+R=\dfrac{1}{2}g\sin\theta \cdot t^{2}$,$R=v_{2}t$
解得$v_{2}=\dfrac{1}{4}\sqrt{gR\sin\theta}$④
联立①②④可得$\dfrac{m_{1}}{m_{2}}=\dfrac{1}{7}$;
在满足($2$)中质量比值的条件下,若碰撞后小球乙能穿过线段$de$,求小球甲初动能应满足的条件。
$\\dfrac{17}{2}m_{1}gR\\sin\\theta{\\lt }E_{{k0}}{\\lt }16m_{1}gR\\sin\\theta$。
"]]在($2$)问的质量比条件下,若碰后乙能越过线段$de$,根据前面分析可知当满足第一种情况时,碰后乙做圆周运动显然不满足能越过线段$de$,故碰后乙做类平抛运动越过线段$de$,故碰后乙的速度必然满足$v_{2}{\lt }\sqrt{gR\sin\theta}$
同时根据类平抛运动规律可知$7R+R=\dfrac{1}{2}g\sin\theta \cdot \Delta t^{2}$,$v_{2}\Delta t\gt R$
解得$\dfrac{1}{4}\sqrt{gR\sin\theta}{\lt }v_{2}{\lt }\sqrt{gR\sin\theta}$⑤
联立②⑤将$\dfrac{m_{1}}{m_{2}}=\dfrac{1}{7}$代入可得$\sqrt{gR\sin\theta}{\lt }v_{1}{\lt 4}\sqrt{gR\sin\theta}$⑥
对甲球从$a$到$c$过程中根据动能定理$- m_{1}g \cdot 8R\sin\theta=\dfrac{1}{2}m_{1}{v_{1}}^{2}-E_{{k0}}$⑦
联立⑥⑦可得$\dfrac{17}{2}m_{1}gR\sin\theta{\lt }E_{{k0}}{\lt }16m_{1}gR\sin\theta$。
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
