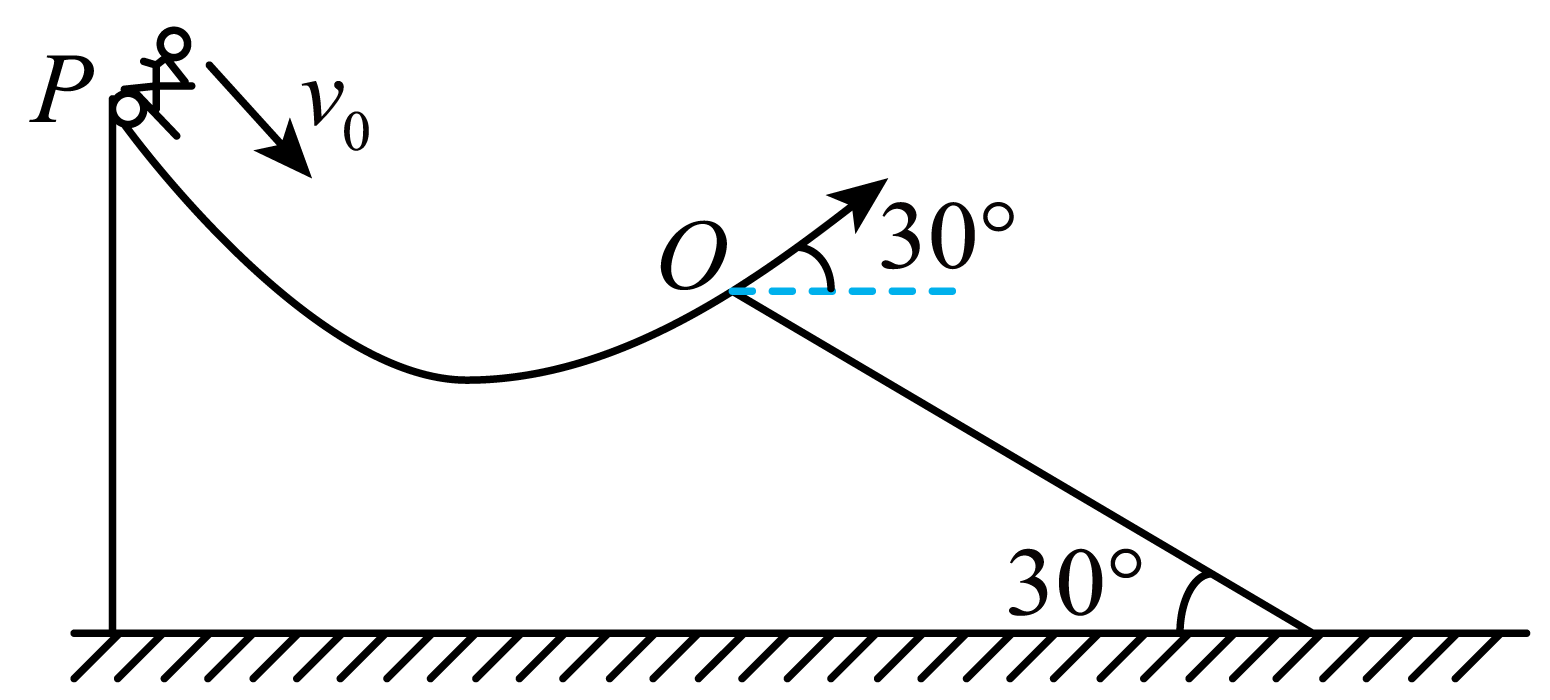
滑滑板是一项青少年酷爱的运动，依靠自身的体能，展现快速的运动艺术。如图所示，一少年在一次训练中以速度$v_{0}=3\;\rm m/s$从$P$点沿切线进入曲面轨道，从$O$点离开曲面轨道，离开$O$点时的速度与水平方向夹角为$30^\circ $，再经过$1\;\rm s$落在倾角为$30^\circ $的斜面上$Q$点（$Q$点未标出）。已知重力加速度$g$取$10\;\rm m/s^{2}$，$P$点到$O$点的竖直高度$h=0.86\;\rm m$，少年和滑板（可视为质点）总质量$m=50\;\rm kg$，忽略空气阻力。少年在此运动过程中，下列说法错误的是$(\qquad)$

从$O$点到$Q$点的距离为$5\\;\\rm m$

在曲面轨道上克服摩擦力做的功为$30\\;\\rm J$

少年落在$Q$点前瞬间重力的功率为$3750\\;\\rm W$

少年离斜面的最大距离为$1\\;\\rm m$

$\rm A$．少年由$O$到$Q$的过程做平抛运动，将此运动沿水平方向与竖直方向分解，如图$1$所示

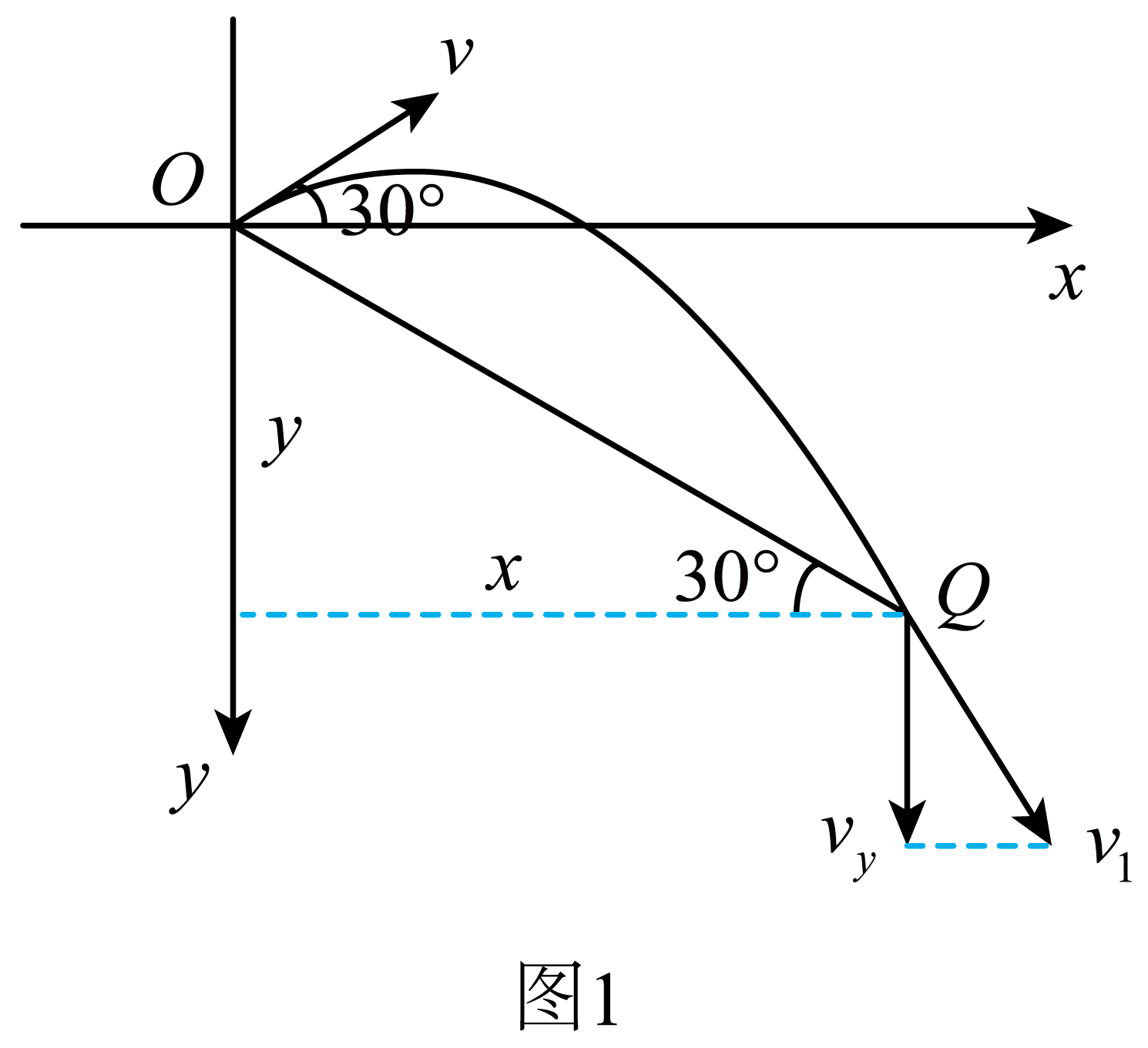
设$O$点的速度大小为$v$，其水平分速度大小为$v\cos30^\circ $，竖直分速度大小为$v\sin30^\circ $，从$O$到$Q$水平方向做匀速直线运动，可得$x=v\cos30^\circ⋅t$

竖直方向做竖直上抛运动，可得$y=- v\sin30{^\circ} \cdot t+\dfrac{1}{2}gt^{2}$

由几何关系得$\dfrac{y}{x}=\tan30{^\circ}$

又已知$t=1\;\rm s$

联立解得$v=5\;\rm m/s$，$x=\dfrac{5\sqrt{3}}{2}\;\text{m}$，$y=2.5\ \rm m$

由几何关系得$O$点到$Q$点的距离$x_{OQ}=\dfrac{y}{\sin30{^\circ}}=\dfrac{2.5}{\sin30{^\circ}}\text{m}=5\;\rm \text{m}$

故$\rm A$正确，不符合题意；

$\rm B$．设在曲面轨道上克服摩擦力做的功为$W$，对此过程，根据动能定理得$mgh-W=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}$

解得$W=30\;\rm J$

故$\rm B$正确，不符合题意；

$\rm C$．少年落在$Q$点前瞬间的竖直分速度大小为$v_{y}=- v\sin30{^\circ}+gt=- 5 \times \dfrac{1}{2}\;\text{m}/\text{s}+10 \times 1\;\rm \text{m}/\text{s}=7.5\;\rm \text{m}/\text{s}$

此时重力的功率为$P=mgv_{y}=50\times10\times7.5\;\rm W=3750\;\rm W$

故$\rm C$正确，不符合题意；

$\rm D$．由$O$到$Q$的过程，少年在垂直于斜面的方向上速度减到零时，其离斜面的距离最远，将$O$到$Q$的运动沿垂直于斜面与平行于斜面分解，如图$2$所示

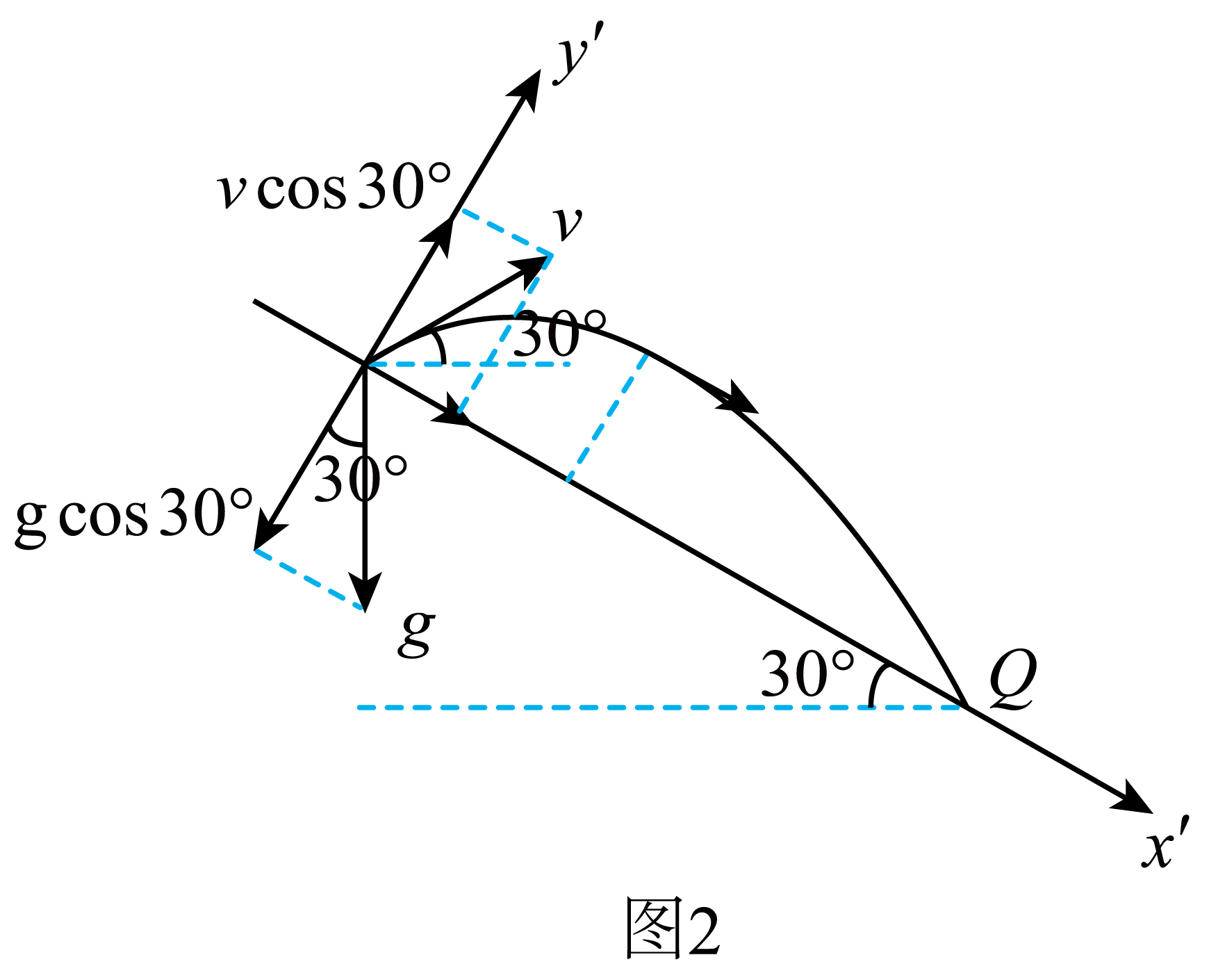
$O$点的速度$v$和重力加速度$g$垂直于斜面的分量分别为$v\cos30^\circ $、$g\cos30^\circ $。

设少年离斜面的最大距离为$y_{m}$，在垂直于斜面的方向上，由运动学公式得$y_{\text{m}}=\dfrac{(v\cos30{^\circ})^{2}}{2g\cos30{^\circ}}$

解得$y_{\text{m}}=\dfrac{5\sqrt{3}}{8}\text{m}$

故$\rm D$错误，符合题意。

本题选错误的，故选：$\rm D$。