高中 | 运动的合成与分解 题目答案及解析
稿件来源:高途
高中 | 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
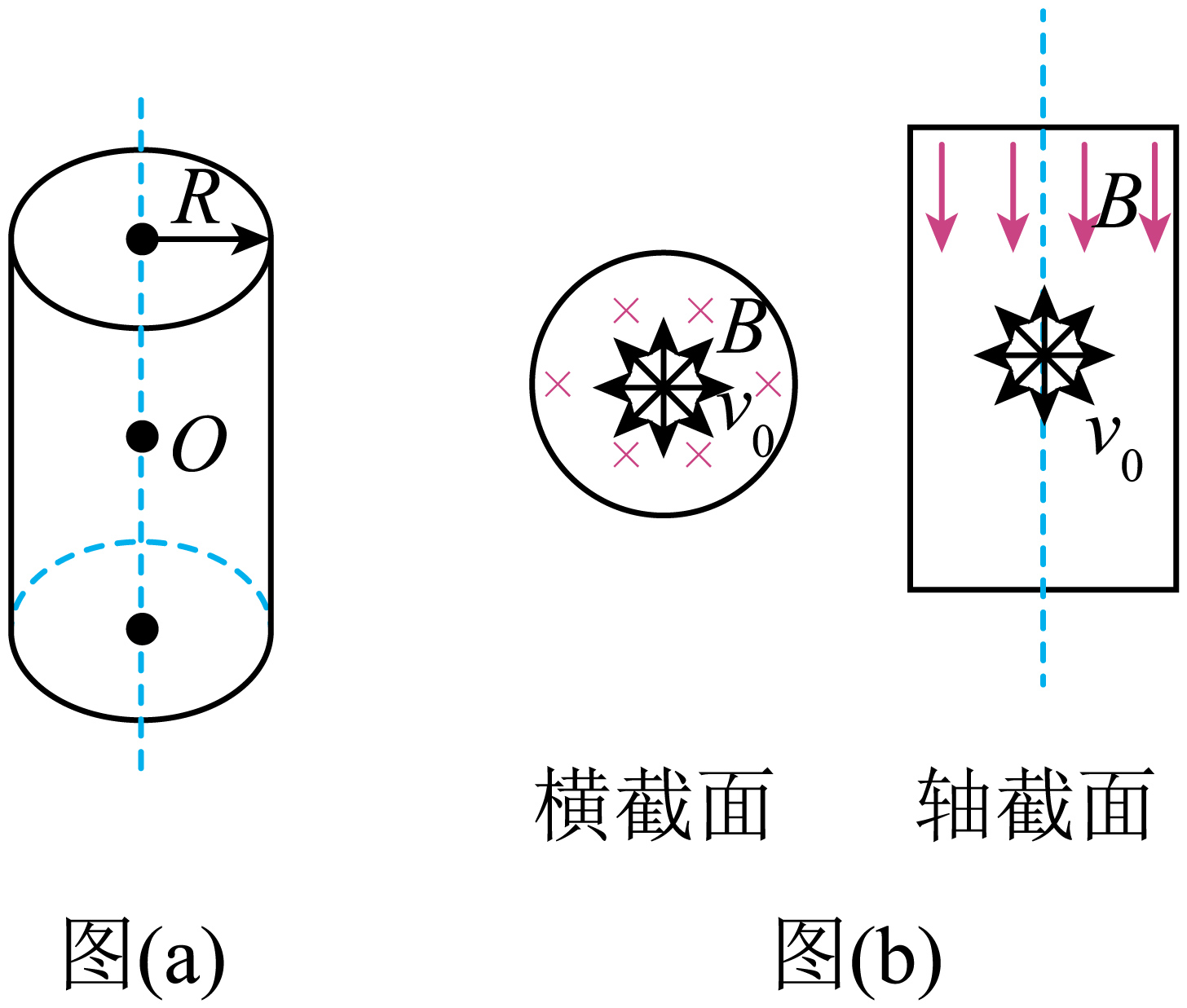
电子比荷是描述电子性质的重要物理量。在标准理想二极管中利用磁控法可测得比荷,一般其电极结构为圆筒面与中心轴线构成的圆柱体系统,结构简化如图($a$)所示,圆筒足够长。在$O$点有一电子源,向空间中各个方向发射速度大小为$v_{0}$的电子,某时刻起筒内加大小可调节且方向沿中心轴向下的匀强磁场,筒的横截面及轴截面示意图如图($b$)所示,当磁感应强度大小调至$B_{0}$时,恰好没有电子落到筒壁上,不计电子间相互作用及其重力的影响。求:($R$、$v_{0}$、$B_{0}$均为已知量)
电子的比荷$\dfrac{e}{m}$;
$\\dfrac{e}{m}= \\dfrac{2v_{0}}{B_{0}R}$;
"]]当磁场的磁感应强度为$B_{0}$时,电子刚好不会落到筒壁上。
则电子以速度$v_{0}$垂直轴线方向射出,电子在磁场中做匀速圆周运动,轨迹恰好与圆筒壁相切,轨迹半径为$R_{0}=\dfrac{R}{2}$
根据洛伦兹力提供向心力可得$eB_{0}v_{0}=\dfrac{m{v_{0}}^{2}}{R_{0}}$
联立解得$\dfrac{e}{m}=\dfrac{2v_{0}}{B_{0}R}$;
当磁感应强度大小调至$\dfrac{1}{2}B_{0}$时,筒壁上落有电子的区域面积$S$。
$S=2\\sqrt{3}\\pi^{2}R^{2}$。
"]]磁感应强度调整为$\dfrac{B_{0}}{2}$后,将电子速度沿垂直轴线和平行轴线方向进行分解,分别设$v_{x}$,$v_{y}$,电子将在垂直轴线方向上做匀速圆周运动,平行轴线方向上做匀速直线运动,电子击中筒壁距离粒子源的最远点时,其垂直轴线方向的圆周运动轨迹与筒壁相切,则轨迹半径仍为$R_{0}=\dfrac{R}{2}$
根据洛伦兹力提供向心力可得$e\dfrac{B_{0}}{2}v_{x}=\dfrac{m{v_{x}}^{2}}{R_{0}}$
联立解得$v_{x}=\dfrac{v_{0}}{2}$
由射出到相切,经过半个周期,用时$t=\dfrac{T}{2}=\dfrac{1}{2} \times \dfrac{2\pi m}{e\dfrac{B_{0}}{2}}=\dfrac{2\pi m}{eB_{0}}=\dfrac{\pi R}{v_{0}}$
根据速度的合成与分解可知$v_{y}=\sqrt{{v_{0}}^{2}-{v_{x}}^{2}}=\dfrac{\sqrt{3}}{2}v_{0}$
平行轴线方向运动距离$y=v_{y}t=\dfrac{\sqrt{3}\pi}{2}R$
结合对称性,被电子击中的面积$S=2 \times 2\pi Ry=2\sqrt{3}\pi^{2}R^{2}$。
高中 | 运动的合成与分解题目答案及解析(完整版)
