高中 | 运动的合成与分解 题目答案及解析
稿件来源:高途
高中 | 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
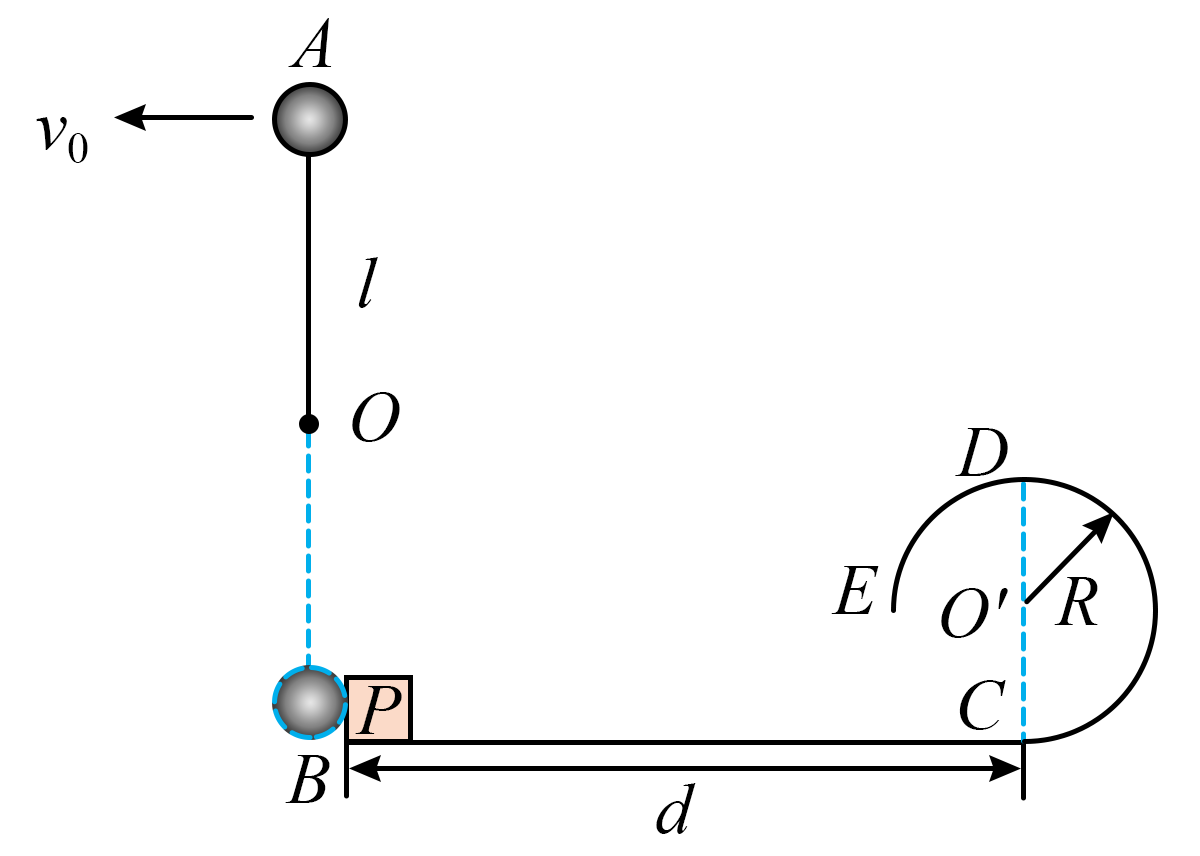
如图所示,长为$l$的轻绳一端固定在$O$点,另一端拴一质量为$m$的小球,$O$点下方固定有一个滑槽装置,由水平直轨道和竖直圆弧轨道组成。其中$BC$段为粗糙水平轨道,长度为$d$,$CDE$部分为光滑圆弧轨道,半径为$R$,$B$点在$O$点正下方,$D$点为圆弧最高点,$E$点和圆心$O$等高。现将球拉至最高点$A$,以$v_{0} = \sqrt{\dfrac{gl}{2}}$的速度向左水平抛出。当小球运动至最低点时,与静止在$B$点的一质量为$m$的滑块$P$发生弹性正碰。碰撞后滑块$P$沿$BC$滑向圆弧轨道$CDE$。滑块和小球均视为质点,重力加速度为$g$,求:
小球抛出后,经过多长时间绳子被拉直?
$t = \\sqrt{\\dfrac{2l}{g}}$
"]]由于$v_{0} = \sqrt{\dfrac{gl}{2}} \lt \sqrt{gl}$,故小球抛出后做平抛运动;
设绳子恰好拉直时绳子与水平方向的夹角为$\theta$,平抛运动的时间为$t$,则有
水平位移$x$ $=$ $l\cos\theta$ $=$ $v_{0}t$,
竖直位移$y = l - l\sin\theta = \dfrac{1}{2}gt^{2}$,
根据勾股定理$l^{2}=x^{2}+y^{2}$
解得$t = \sqrt{\dfrac{2l}{g}}$,即当小球运动到绳子刚好处于水平位置时被拉直;
设绳子被拉直瞬间,小球沿绳子方向的分速度突变为零,则小球第一次运动到$B$点的速度$v_{B}$大小为多少?
$v_{B} = 2\\sqrt{gl}$
"]]在绳子拉直瞬间,小球沿绳子方向的速度立即消失,只余竖直方向的速度$v_{y} = gt = \sqrt{2gl}$
此后小球做圆周运动,从拉直瞬间到运动到最低点$B$,由动能定理可得$mgl = \dfrac{1}{2}mv_{B}^{2} - \dfrac{1}{2}mv_{y}^{2}$,解得$v_{B} = 2\sqrt{gl}$;
要使滑块能滑上圆弧轨道且在圆弧轨道运动时不脱离,则水平轨道$BC$段的摩擦因数$\mu $取值范围是多少?
$0\\lt\\mu\\leqslant\\dfrac{4l-5R}{2d}$或者$\\dfrac{2l-R}{d}\\leqslant\\mu\\lt\\dfrac{2l}{d}$
"]]当小球与滑块发生弹性碰撞过程中,由小球和滑块组成的系统动量守恒、机械能守恒。设碰后小球速度为$v_{1}$,滑块速度为$v_{2}$,
有$mv_{B} = mv_{1} + mv_{2}$,$\dfrac{1}{2}mv_{B}^{2} = \dfrac{1}{2}mv_{1}^{2} + \dfrac{1}{2}mv_{2}^{2}$,解得$v_{2} = 2\sqrt{gl}$
要使滑块不脱离轨道$CDE$,有两种情况:
①滑块能在圆弧轨道$CDE$做完整的圆周运动,则滑块从$B$点运动到圆轨道最高点$D$的过程中,由动能定理可得$- \mu mgd - mg \cdot 2R = \dfrac{1}{2}mv_{D}^{2} - \dfrac{1}{2}mv_{2}^{2}$
在$D$点时$mg\leqslant\dfrac{mv_{D}^{2}}{R}$,解得$0\lt\mu\leqslant\dfrac{4l-5R}{2d}$;
②滑块最高运动到与圆心$O^\prime$等高处及以下位置,速度恰好为零,沿轨道返回,
设滑块上升的最大高度为$h$,则有$- \mu mgd - mgh = 0 - \dfrac{1}{2}mv_{2}^{2}$,$h\leqslant R$,解得$\mu\geqslant\dfrac{2l-R}{d}$
滑块能滑到圆弧轨道,则有$\dfrac{1}{2}mv_{2}^{2}-\mu mgd\gt0$,解得$\mu\lt\dfrac{2l}{d}$
即当水平轨道$BC$段的摩擦因数$\mu $满足$0\lt\mu\leqslant\dfrac{4l-5R}{2d}$或者$\mu\geqslant\dfrac{2l-R}{d}$时,滑块始终不脱离圆轨道。
高中 | 运动的合成与分解题目答案及解析(完整版)
