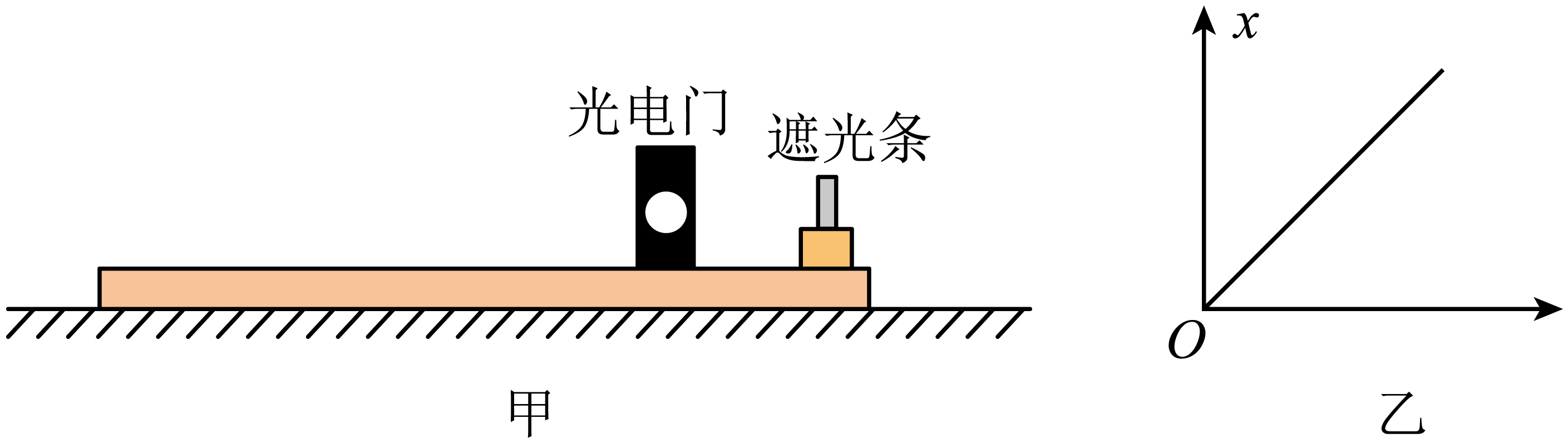
实验前测得遮光条的宽度为$d$，含遮光条的滑块质量为$m$，则滑块经过光电门时的动能$E_{\rm k}=$                 （用给定的物理量符号表示）。

滑块经过光电门时的速度大小$v= \dfrac{d}{t}$

由公式知$E_{\text{k}}=\dfrac{1}{2}mv^{2}$

代入得$E_{\text{k}}=\dfrac{1}{2}m\left( \dfrac{d}{t} \right)^{2}=\dfrac{md^{2}}{2t^{2}}$

实验时获得多组数据后，得出的图像如图乙所示，该图像的纵坐标为$x$，则横坐标为                 （填“ $\dfrac{1}{t}$”“ $t^{2}$”或“ $\dfrac{1}{t^{2}}$”）。若直线的斜率为$k$，则滑块与木板之间的动摩擦因数$\mu =$                 （用题中物理量的符号$d$，$k$和$g$表示）。

根据动能定理有$- \mu mgx=0- \dfrac{1}{2}mv^{2}$

整理得$\mu=\dfrac{\dfrac{1}{2}mv^{2}}{mgx}=\dfrac{d^{2}}{2gxt^{2}}$

变形得$x=\dfrac{d^{2}}{2g\mu} \cdot \dfrac{1}{t^{2}}$

由表达式可知，横坐标为$\dfrac{1}{t^{2}}$。

若直线的斜率为$k$，根据表达式可知，则滑块与木板之间的动摩擦因数为$\mu=\dfrac{d^{2}}{2gk}$