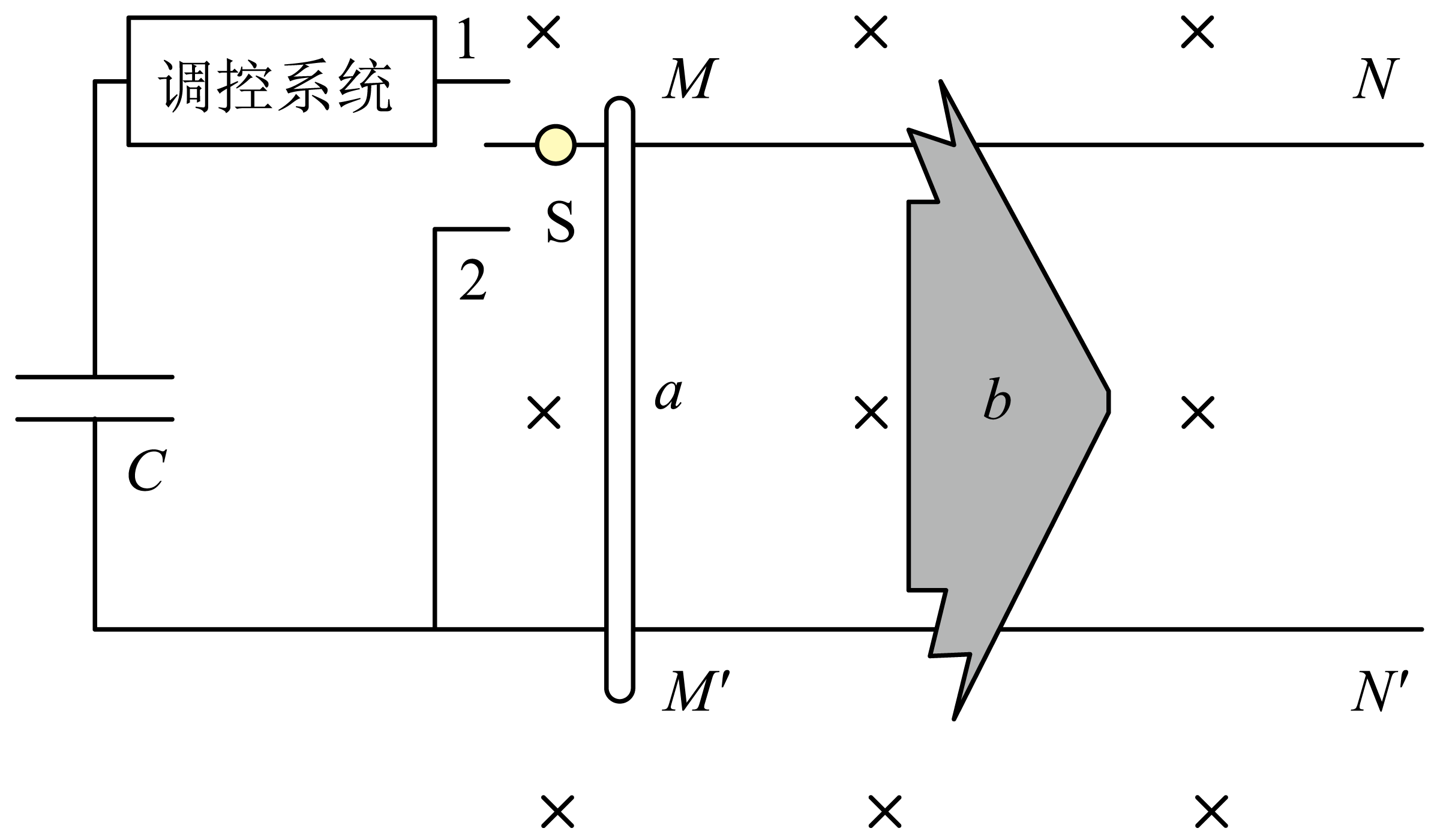
若分离后某时刻$a$的速度大小为$10\;\rm m/s$，求此时通过$a$的电流大小；

$500\\;\\rm A$；

分离后$a$切割磁感线有$E=BLv$

则通过$a$的电流$I=\dfrac{E}{R}$

解得$I=500\;\rm A$；

忽略$a$、$b$所受空气阻力，当$a$与$b$的初始间距为$1.25\;\rm m$时，求$b$分离后的速度大小，分析其是否为$b$能够获得的最大速度；并求$a$运动过程中电容器的电压减小量；

$v_{b1}=25\\;\\rm m/s$，能，$\\Delta U=40\\;\\rm V$；

由于超级电容器经调控系统为电路提供$I_{0}=1000\;\rm A$的恒定电流，则当$a$与$b$的初始间距为$1.25\;\rm m$时$a$与$b$碰撞前的速度为$BI_{0}Lx_{ab}= \dfrac{1}{2}m_{a}v_{a}^{2}$

$a$与$b$碰撞时根据动量守恒和能量守恒有$m_{a}v_{a}=(m_{a}+m_{b})v_{共}$，$\dfrac{1}{2}m_{a}v_{a}^{2}=\dfrac{1}{2}(m_{a}+m_{b})v_{共}^{2}+E_{\rm{p}}$

$a$与$b$整体从$MM'$到$NN'$的过程中有$BI_{0}L(x_{MN}-x_{ab})=\dfrac{1}{2}(m_{a}+m_{b})v_{共1}^{2}-\dfrac{1}{2}(m_{a}+m_{b})v_{共}^{2}$

$a$与$b$分离时根据动量守恒和能量守恒有$(m_{a}+m_{b})v_{共1}=m_{a}v_{a1}+m_{b}v_{b1}$，$\dfrac{1}{2}(m_{a}+m_{b})v_{共1}^{2}+E_{\rm{p}}=\dfrac{1}{2}m_{a}v_{a1}^{2}+\dfrac{1}{2}m_{b}v_{b1}^{2}$

联立解得$v_{b1}=25\;\rm m/s$

由于$a$和$ab$组合体均做匀变速直线运动，分别有$x_{ab}=\dfrac{v_{a}}{2}t_{1}$，$x_{MN}-x_{ab}=\dfrac{v_{共}+v_{共1}}{2}t_{2}$

则电容器流出的电荷量有$\Delta q=I_{0}(t_{1}+t_{2})$

$a$运动过程中电容器的电压减小量$\Delta U=\dfrac{\Delta q}{C}=40\;\rm{V}$；

忽略$a$所受空气阻力，若$b$所受空气阻力大小与其速度$v$的关系为$f$ $=kv^{2}$（$k=$ $0.025\;\rm N·s^{2}/m^{2}$），初始位置与（$2$）问一致，试估算$a$运行至$NN'$时。$a$分离前的速度大小能否达到（$2$）问中分离前速度的$99\%$，并给出结论。（$0.99^{2}=0.980l$）

能。

$b$所受$f=kv^{2}(k=0.025\;\rm N·s^{2}/m^{2}$）的空气阻力后，$a$与$b$整体从$MM'$到$NN'$的过程中有$(BI_{0}L-kv^{2})=(m_{a}+m_{b})a$，$a=v\dfrac{\Delta v}{\Delta x}$

求解出$v_{共2}=\sqrt{392.64}\;\rm{m/s}$

则$\dfrac{v_{共2}}{v_{共1}} \approx 99.05\%$

$a$分离前的速度大小能达到（$2$）问中分离前速度的$99\%$。