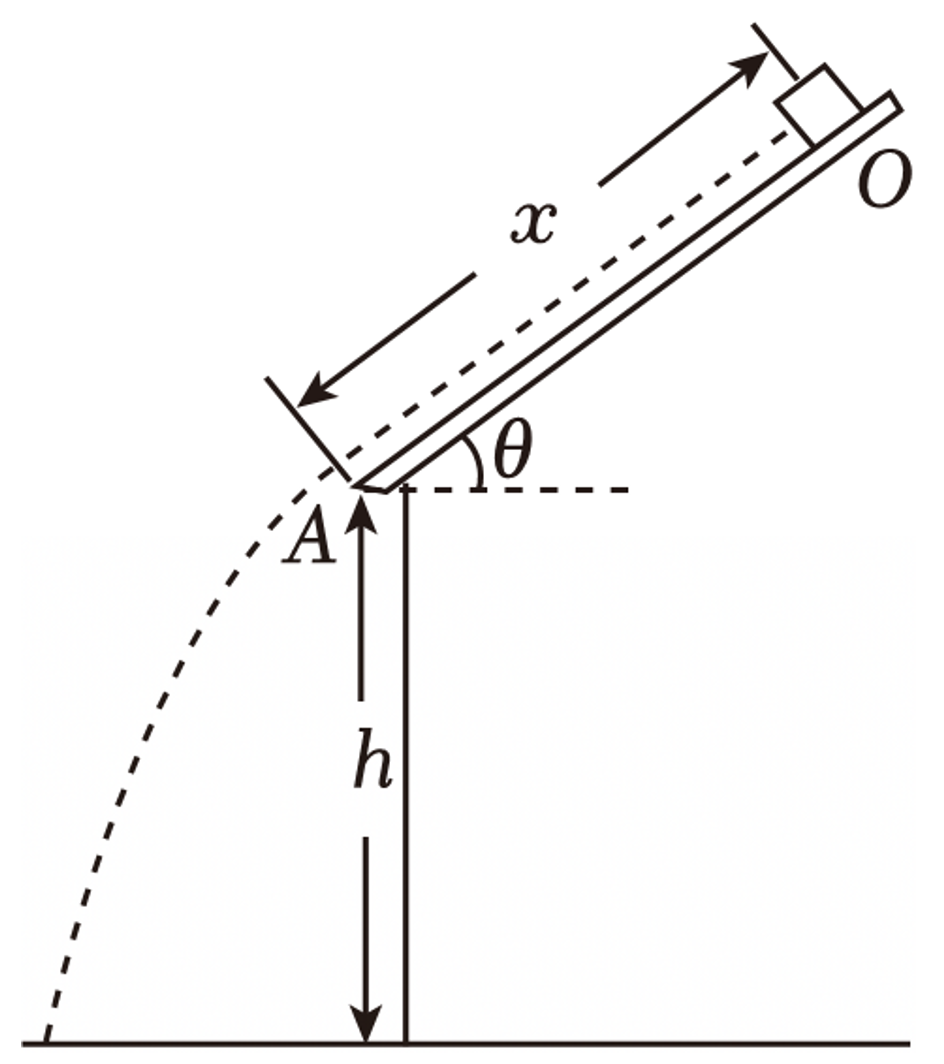
雪块从$A$点离开屋顶时的速度大小$v_{0}$；

$5\\;\\rm m/s$；

雪块在屋顶上运动过程中，由动能定理$mgx\sin\theta-\mu mg\cos\theta \cdot x= \dfrac{1}{2}mv_{0}^{2}-0$

代入数据解得雪块到$A$点速度大小为$v_{0}=5\;\rm m/s$；

雪块落地时的速度大小$v_{1}$，及其速度方向与水平方向的夹角$\alpha$。

$8\\;\\rm m/s$，$60^\\circ$。

雪块离开屋顶后，做斜下抛运动，由动能定理$mgh=\dfrac{1}{2}mv_{1}^{2}- \dfrac{1}{2}mv_{0}^{2}$

代入数据解得雪块到地面速度大小$v_{1}=8\;\rm m/s$

速度与水平方向夹角$\alpha$，满足$\cos\alpha=\dfrac{v_{0}\cos\theta}{v_{1}}=\dfrac{5 \times 0.8}{8}=\dfrac{1}{2}$

解得$\alpha=60^\circ $。