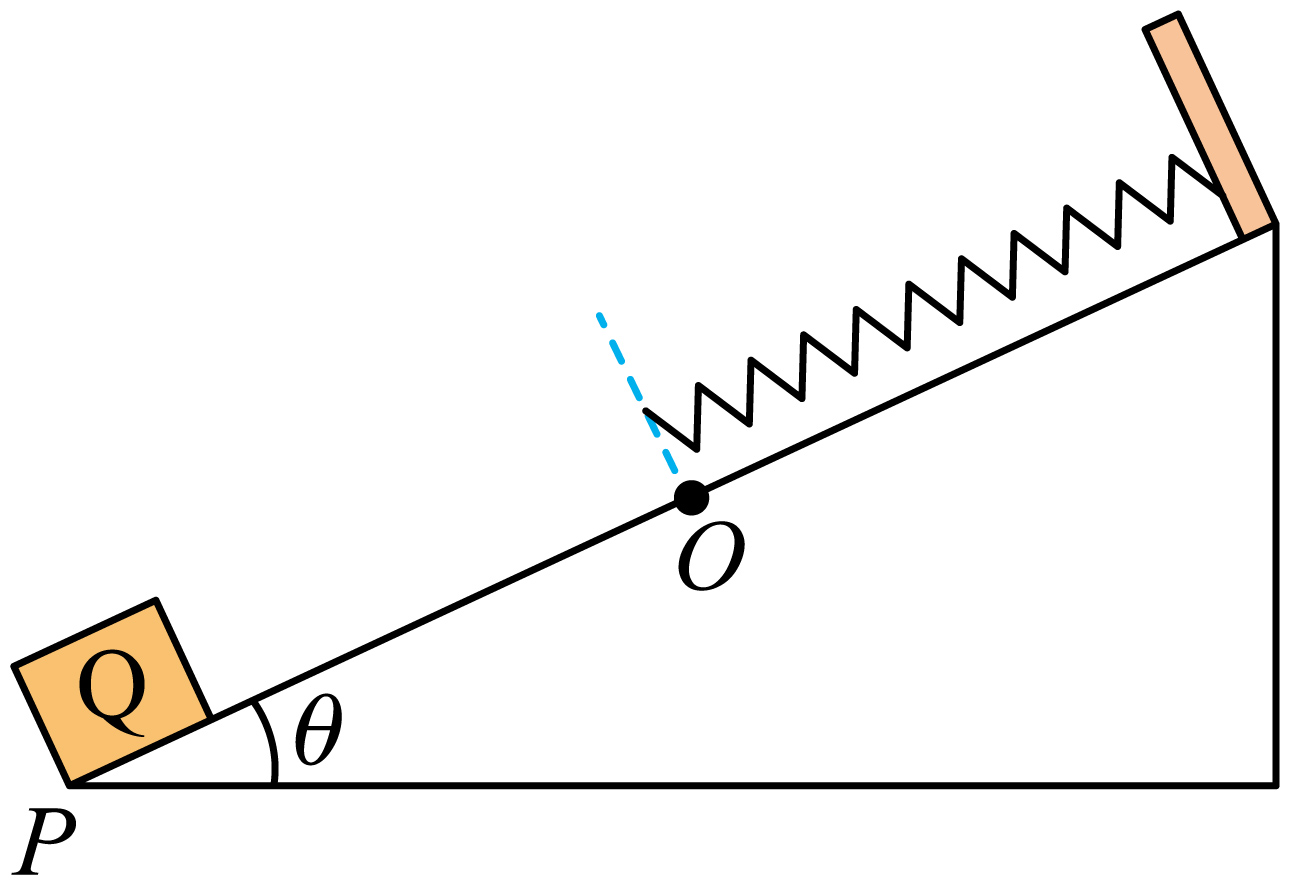
如图所示，倾角为$\theta$的固定斜面，其顶端固定一劲度系数为$k$的轻质弹簧，弹簧处于原长时下端位于$O$点。质量为$m$的滑块$Q$（视为质点）与斜面间的动摩擦因数$\mu =\tan \theta$。过程Ⅰ：$Q$以速度$v_{0}$从斜面底端$P$点沿斜面向上运动恰好能滑至$O$点；过程Ⅱ：将$Q$连接在弹簧的下端并拉至$P$点由静止释放，$Q$通过$M$点（图中未画出）时速度最大，过$O$点后能继续上滑。弹簧始终在弹性限度内，假设最大静摩擦力等于滑动摩擦力，忽略空气阻力，重力加速度为$g$。则$(\qquad)$

$P$、$M$两点之间的距离为$\\dfrac{kv_{0}^{2}-4mg^{2}\\sin^{2}\\theta}{4kg\\sin\\theta}$

过程Ⅱ中，$Q$在从$P$点单向运动到$O$点的过程中损失的机械能为$\\dfrac{1}{4}mv_{0}^{2}$

过程Ⅱ中，$Q$从$P$点沿斜面向上运动的最大位移为$\\dfrac{kv_{0}^{2}-8mg^{2}\\sin^{2}\\theta}{2 kg\\sin\\theta}$

连接在弹簧下端的$Q$无论从斜面上何处释放，最终一定静止在$OM$（含$O$、$M$点）之间

$\rm A$．设$PO$的距离为$L$，过程$I$，根据动能定理有$- mg\sin\theta \cdot L-\mu mg\cos\theta \cdot L=0-\dfrac{1}{2}mv_{0}^{2}$

设$MO$的距离为$L_{1}$，过程Ⅱ中，当$Q$速度最大时，根据平衡条件$kL_{1}=mg\sin \theta+\mu mg\cos \theta$

$P$、$M$两点之间的距离$L_{2}=L − L_{1}$

联立可得$kL_{2}=\dfrac{kv_{0}^{2}-4mg^{2}\sin^{2}\theta}{2kg\sin\theta}$

故$\rm A$错误；

$\rm B$．根据功能关系，可知过程Ⅱ中，$Q$在从$P$点单向运动到$O$点的过程中损失的机械能$\Delta E=\mu mg\cos \theta ⋅ L$

结合$- mg\sin\theta \cdot L-\mu mg\cos\theta \cdot L=0-\dfrac{1}{2}mv_{0}^{2}$

可得$\Delta E=\dfrac{1}{4}mv_{0}^{2}$

故$\rm B$正确；

$\rm C$．设过程Ⅱ中，$Q$从$P$点沿斜面向上运动的最大位移$x$，根据能量守恒定律$\dfrac{1}{2}kL^{2}=mg\sin\theta \cdot x+\mu mg\cos\theta \cdot x+\dfrac{1}{2}k{(x-L)}^{2}$

结合$- mg\sin\theta \cdot L-\mu mg\cos\theta \cdot L=0-\dfrac{1}{2}mv_{0}^{2}$

解得$x=\dfrac{kv_{0}^{2}-8mg^{2}\sin^{2}\theta}{2kg\sin\theta}$

故$\rm C$正确；

$\rm D$．无论$Q$从何处释放，$Q$在斜面上运动过程中，弹簧与$Q$初始时的势能变为摩擦热，当在$M$点时，满足$kL_{1}=mg\sin \theta+\mu mg\cos \theta$

当在$O$点时，满足$mg\sin \theta=\mu mg\cos \theta$

所以在$OM$（含$O$、$M$点）之间速度为零时，$Q$将静止，故$\rm D$正确。

故选：$\rm BCD$。