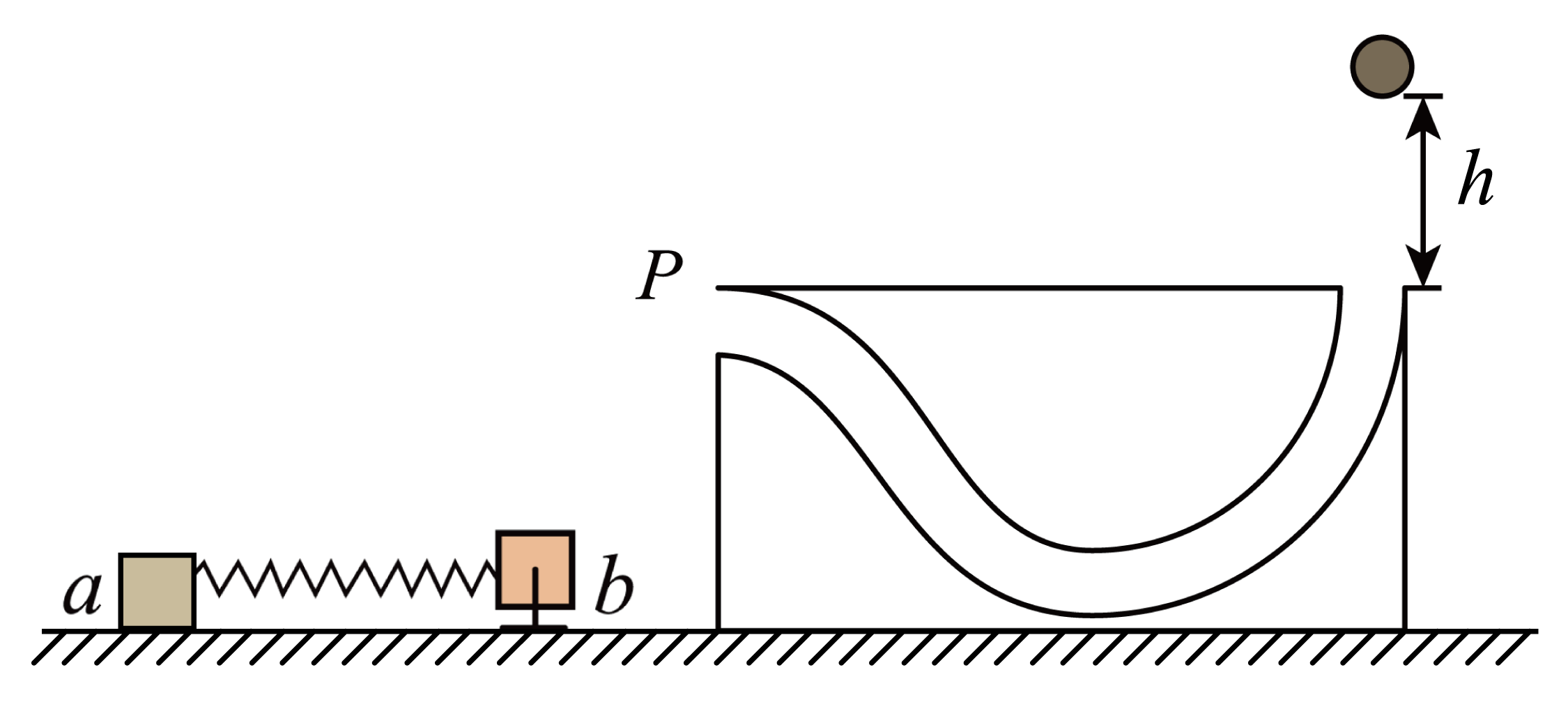
小球到达$P$点时，小球及方形物体相对于地面的速度大小$v_{1}$、$v_{2}$；

$6\\;\\rm m/s$，水平向左，$\\dfrac{2}{3}\\;\\rm m/s$，水平向右；

根据题意可知，小球从开始下落到$P$处过程中，水平方向上动量守恒，则有$mv_{1}=Mv_{2}$

由能量守恒定律有$mgh=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}Mv_{2}^{2}$

联立解得$v_{1}=6\;\rm m/s$，$v_{2}=\dfrac{2}{3}\;\rm m/s$

即小球速度为$6\;\rm m/s$，方向水平向左，大物块速度为$\dfrac{2}{3}\;\rm m/s$，方向水平向右；

弹簧弹性势能最大时，$b$的速度大小$v_{b}$及弹性势能的最大值$E_\rm{pm}$。

$\\dfrac{2}{3}\\;\\rm m/s$，水平向左，$E_{\\rm{pm}}=\\dfrac{5}{2}\\;\\rm {J}$。

由于小球落在物块$a$正上方，并与其粘连，小球竖直方向速度变为$0$，小球和物块$a$水平方向上动量守恒，则有$mv_{1}=(m+m_{a})v_{3}$

解得$v_{3}=2\;\rm m/s$

设当弹簧形变量为$x_{1}$时物块$b$的固定解除，此时小球和物块$a$的速度为$v_{4}$，根据胡克定律$F=kx_{1}$

系统机械能守恒$\dfrac{1}{2}\left( m+m_{a} \right)v_{3}^{2}=\dfrac{1}{2}\left( m+m_{a} \right)v_{4}^{2}+\dfrac{1}{2}kx_{1}^{2}$

联立解得$v_{4}=1\;\rm m/s$，$x_{1}=0.3m$

固定解除之后，小球、物块$a$和物块$b$组成的系统动量守恒，当三者共速时，弹簧的弹性势能最大，由动量守恒定律有$(m+m_{a})v_{4}=(m+m_{a}+m_{b})v_{b}$

解得$v_{b}=\dfrac{2}{3}\;\rm m/s$，方向水平向左。

由能量守恒定律可得，最大弹性势能为$E_{\rm{pm}}=\dfrac{1}{2}\left( m+m_{a} \right)v_{4}^{2}+\dfrac{1}{2}kx_{1}^{2}-\dfrac{1}{2}\left( m+m_{a}+m_{b} \right)v_{b}^{2}=\dfrac{5}{2}\;\rm {J}$。