高中 | 功率的概念与计算 题目答案及解析
稿件来源:高途
高中 | 功率的概念与计算题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.3 功率
功率的概念与计算
如图所示,用开瓶器取出紧塞在瓶口的软木塞时,先将拔塞钻旋入木塞内,随后下压把手,使齿轮绕固定支架上的转轴转动,通过齿轮啮合,带动与木塞相固定的拔塞钻向上运动。从$0$时刻开始,顶部与瓶口齐平的木塞从静止开始向上做匀加速直线运动,木塞所受摩擦力$f$随位移大小$x$的变化关系为$f=f_{0}\left( 1-\dfrac{x}{h} \right)$,其中$f_{0}$为常量,$h$为圆柱形木塞的高,木塞质量为$m$,底面积为$S$,加速度为$a$,齿轮半径为$r$,重力加速度为$g$,瓶外气压减瓶内气压为$\Delta p$且近似不变,瓶子始终静止在桌面上。(提示:可用$f − x$图线下的“面积”表示$f$所做的功)求:
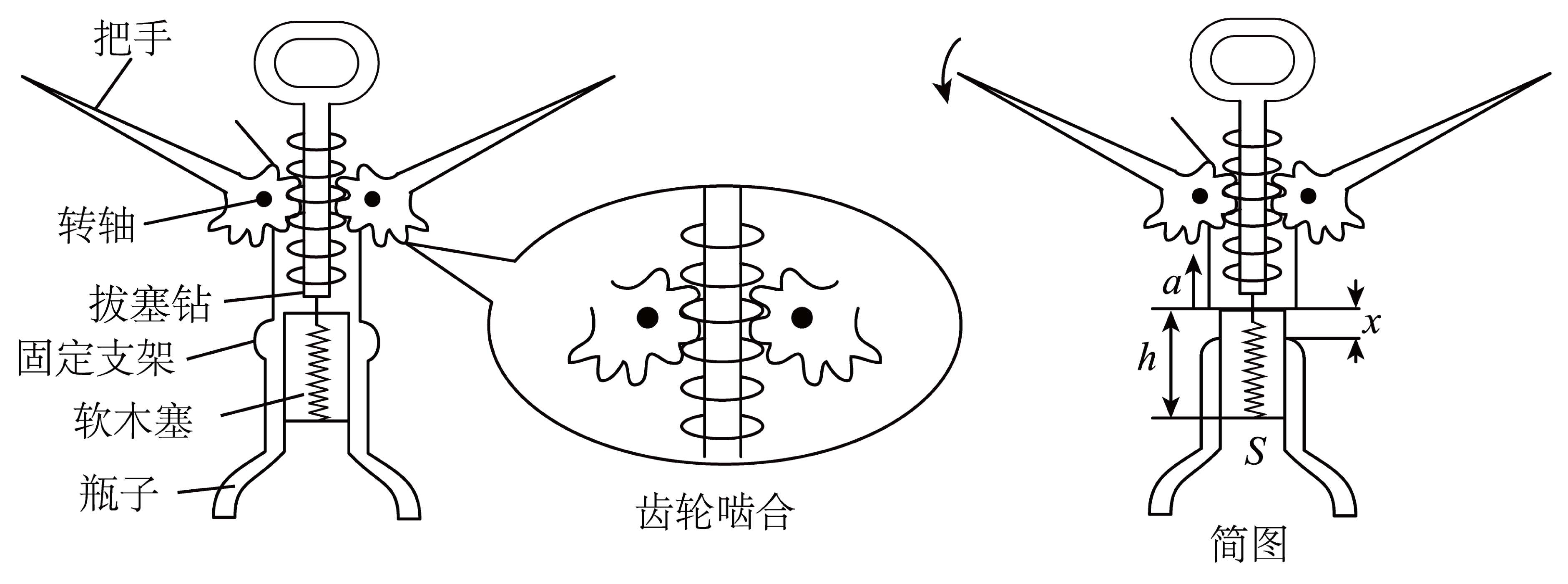
木塞离开瓶口的瞬间,齿轮的角速度$\omega$。
$\\omega= \\dfrac{\\sqrt{2ah}}{r}$
"]]木塞的末速度等于齿轮线速度,对木塞,根据运动学公式$v^{2}=2ah$
根据角速度和线速度的关系$v=\omega r$
联立可得$\omega=\dfrac{\sqrt{2ah}}{r}$
拔塞的全过程,拔塞钻对木塞做的功$W$。
$W=mah+mgh+\\dfrac{1}{2}f_{0}h+ \\Delta pSh$
"]]根据题意画出木塞摩擦力与运动距离的关系图如图所示
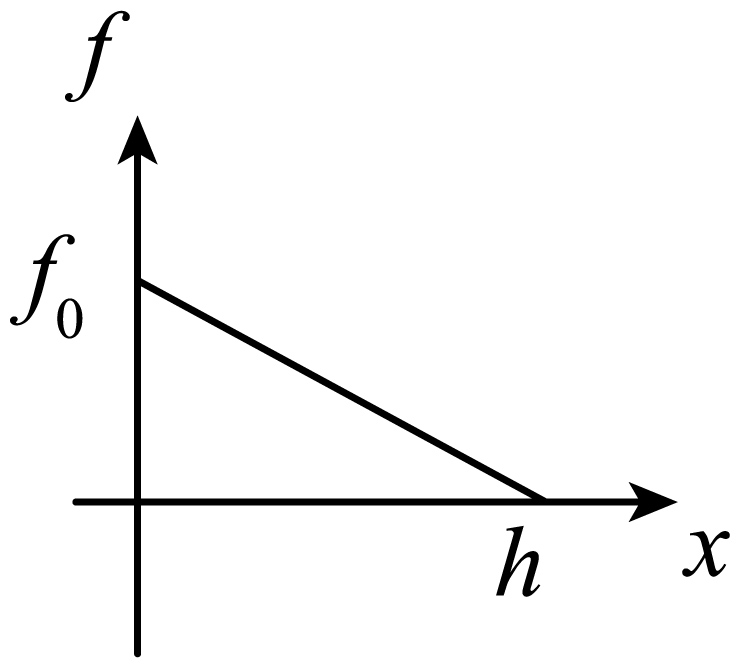
可得摩擦力对木塞所做的功为$W_{{f}}=- \dfrac{1}{2}f_{0}h$
对木塞,根据动能定理$W+W_{{f}}-mgh-\Delta pSh=\dfrac{1}{2}mv^{2}-0$
解得$W=mah+mgh+\dfrac{1}{2}f_{0}h+\Delta pSh$
拔塞过程中,拔塞钻对木塞作用力的瞬时功率$P$随时间$t$变化的表达式。
$P=magt+ma^{2}t+\\Delta pSat+ f_{0}at-\\dfrac{f_{0}a^{2}}{2h} \\times t^{3}$
"]]设开瓶器对木塞的作用力为$F$,对木塞,根据牛顿第二定律$F-mg-f-\Delta pS=ma$
速度$v=at$
位移$x=\dfrac{1}{2}at^{2}$
开瓶器的功率$P=Fv$
联立可得$P=magt+ma^{2}t+\Delta pSat+f_{0}at-\dfrac{f_{0}a^{2}}{2h} \times t^{3}$
高中 | 功率的概念与计算题目答案及解析(完整版)
