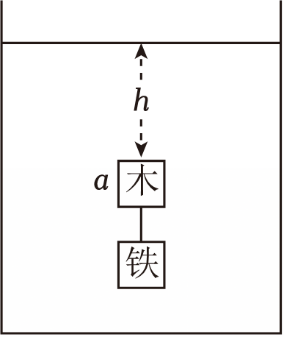
如图，边长均为$a$的立方体木块和空心铁块，用长度也为$a$的细绳连接，悬浮在平静的池中，木块上表面和水面的距离为$h$。当细绳断裂后，木块与铁块分别竖直向上、向下运动，当木块上表面刚浮出水面时，铁块恰好到达池底。已知木块的质量为$m$，铁块的质量为$M$，不计水的阻力，则池深为$(\qquad)$

$\\dfrac{M+m}{M}h$

$\\dfrac{M+m}{M}h+2a$

$\\dfrac{M+m}{M}h+3a$

$\\dfrac{M+m}{M}(h+2a)$

铁块下降的高度为$H$，在整个过程中木块和铁块整体在竖直方向所受合外力为零，对于木块和铁块整体由平均动量守恒有$mh=MH$

池深$h+H+3a=\dfrac{M+m}{M}h+3a$，

故$\rm ABD$错误，$\rm C$正确。

故选：$\rm C$。