如图所示，一轻弹簧竖直放置，两端分别固定物体$B$和$C$，此时$B$、$C$处于静止状态，$O$点是弹簧处于原长时物体$B$上表面所处的位置，$B$、$O$间距离为$x$。把一物体$A$从静止释放，释放时$A$、$B$之间的距离为$h$，物体$A$和物体$B$的质量均为$m$，发生碰撞后粘在一起向下运动（以后不再分开），压缩弹簧然后上升到最高点时，物体$B$的上表面刚好到达$D$点，$O$、$D$之间距离也为$x$，重力加速度为$g$，物体$C$始终静止，下列说法正确的是$(\qquad)$

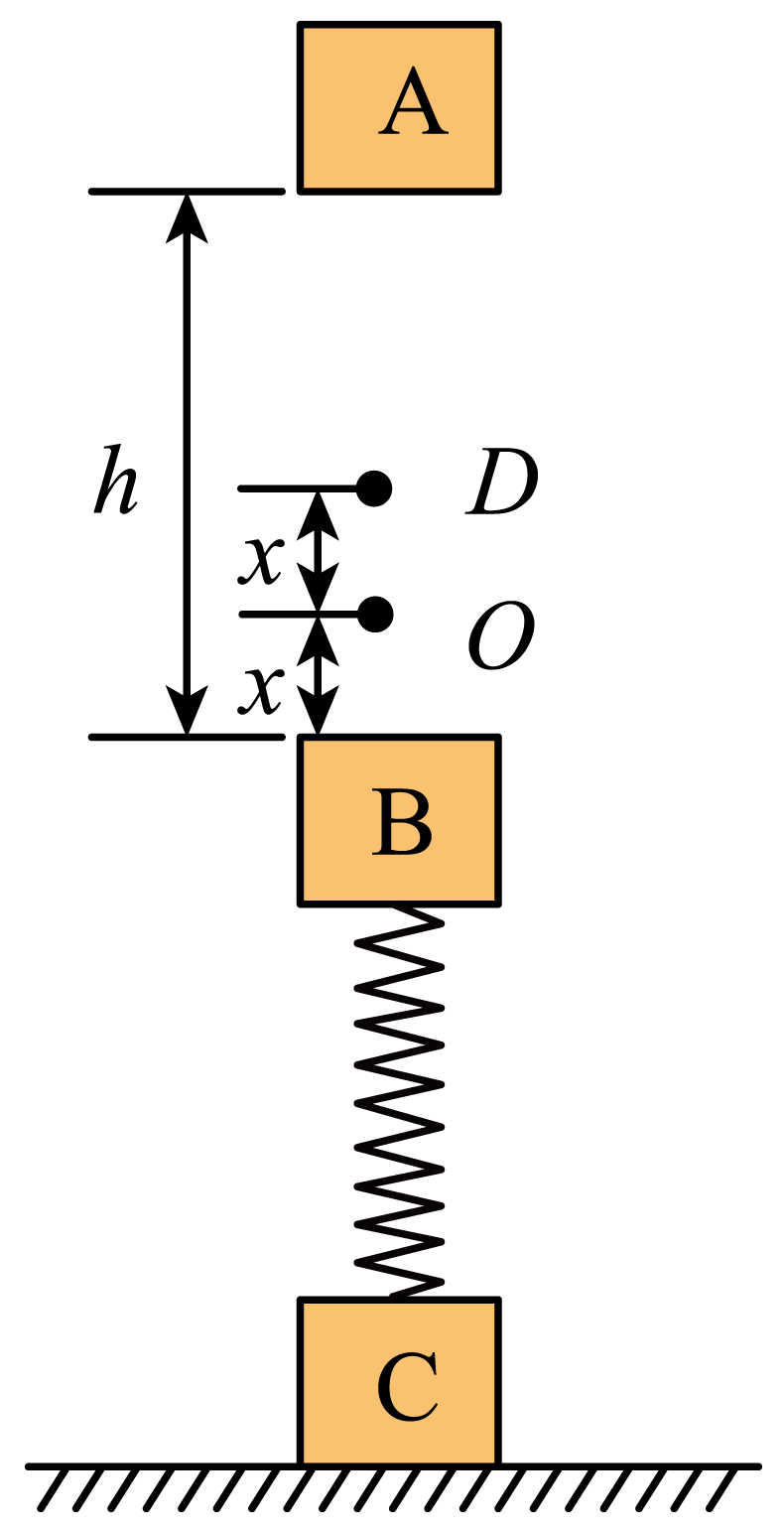
物体$C$的质量不可能等于$m$

运动到$D$点时，$A$、$B$之间弹力为零

碰撞后瞬间物体$B$的速度为$\\dfrac{\\sqrt{2gh}}{2}$

碰撞后$AB$物体做简谐运动的振幅是$2x$

$\rm A$．因为$C$始终静止，当运动至$D$点时，$O$、$D$之间距离也为$x$，由胡克定律可知弹簧的弹力等于物体$B$的受到的重力，所以物体$C$的质量要大于或等于$m$，故$\rm A$错误；

$\rm B$．$A$、$B$运动到$D$点时，弹簧处于拉伸状态，设此时$A$、$B$的共同加速度为$a$，对$A$受力分析，根据牛顿第二定律可得$mg+F_{BA}=ma$

$A$与$B$整体受力分析则有$2mg+k ⋅ x=2ma$

结合上述分析可知$kx=mg$

联立解得$F_{\text{BA}}=\dfrac{1}{2}mg$，故$\rm B$错误；

$\rm C$．由运动学公式$mgh=\dfrac{1}{2}mv_{0}^{2}$

可得碰撞前物体$A$的速度$v_{0}=\sqrt{2gh}$

根据动量守恒定律可得$mv_{0}=2mv$

解得碰撞后瞬间物体$B$的速度为$v=\dfrac{\sqrt{2gh}}{2}$

故$\rm C$正确；

$\rm D$．设$A$、$B$简谐振动的平衡位置距$O$点为$x_{0}$，则有$2mg=kx_{0}$，$mg=kx$

解得$x_{0}=2x$

则碰撞后$AB$物体做简谐运动的振幅是$A=x_{0}+x=3x$，故$\rm D$错误。

故选：$\rm C$。