高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
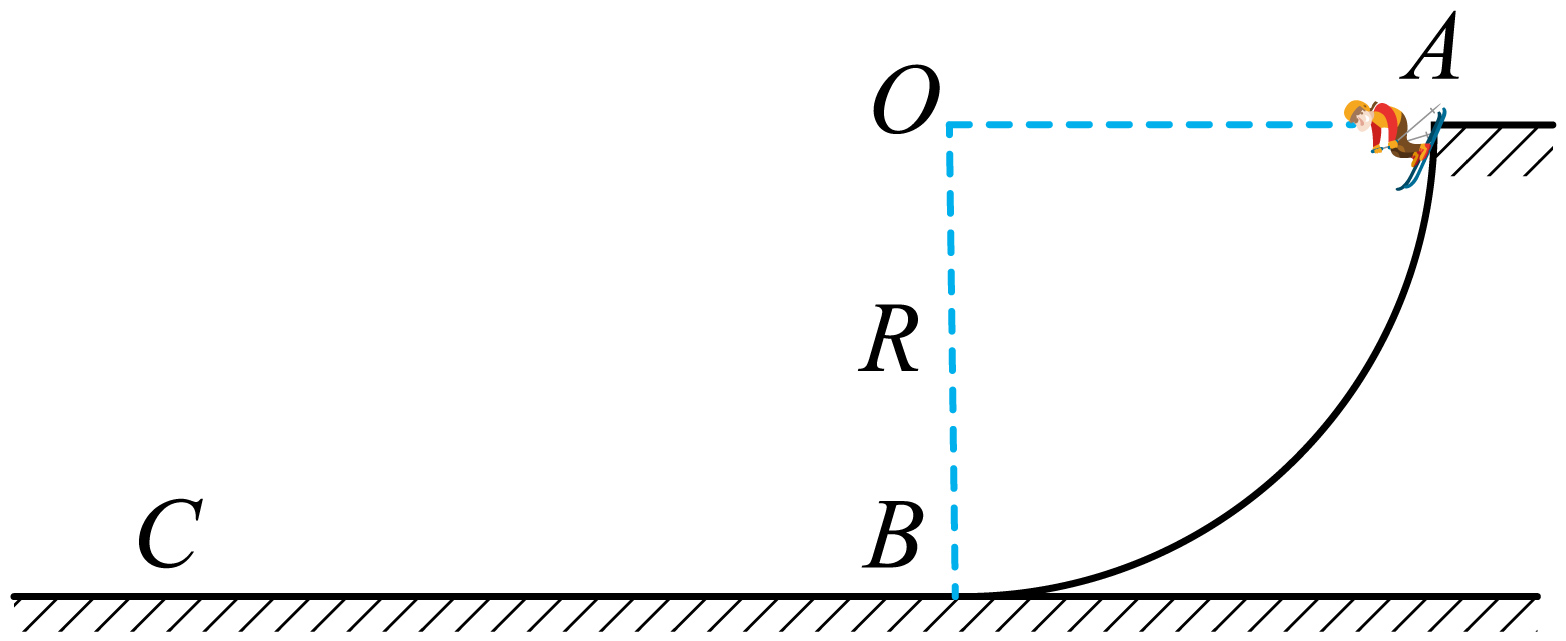
$2025$年$2$月$27$日至$3$月$10$日,第十二届残运会高山滑雪比赛在新疆乌鲁木齐丝绸之路国际滑雪场举行。如图所示为一简化后的滑雪的雪道模型示意图,竖直平面内半径$R=5\ \text{m}$的光滑四分之一圆弧轨道与水平雪道相切于$B$点。质量$m=60\ \text{kg}$的运动员由$A$点静止下滑,最后静止于水平雪道上的$C$点。已知运动员与地面$BC$间的动摩擦因数$\mu=0.25$。运动员可视为质点,忽略空气阻力,重力加速度大小为$g=10\ \text{m}/\text{s}^{2}$,则运动员在$B$点时所受圆弧轨道的支持力大小${{F}_{\text{N}}}$和$B$、$C$两点间的距离$x$分别为$(\quad\ \ \ \ )$
$F_{\\text{N}}=1800\\ \\text{N}$;$x=20\\ \\text{m}$
","$F_{\\text{N}}=1800\\ \\text{N}$;$x=40\\ \\text{m}$
","$F_{\\text{N}}=3600\\text{ N}$;$x=20\\text{\\ m}$
","$F_{\\text{N}}=3600\\ \\text{N}$;$x=40\\ \\text{m}$
"]运动员从$A$到$B$过程,根据机械能守恒定律有$mgR=\dfrac{1}{2}mv_{B}^{2}$,解得得$v_{B}=10\;\text{m}/\text{s}$。运动员在$B$点时,根据牛顿第二定律有${{F}_{\text{N}}}-mg=\dfrac{mv_{B}^{2}}{R}$,解得$F_{\text{N}}=1800\;\text{N}$。运动员由$B$点运动到$C$点的过程中,根据动能定理有$-\mu mgx=0-\dfrac{1}{2}mv_{B}^{2}$,解得$x=20\;\text{m}$。
故选$\rm A$。
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
