地球和月球间的距离为$L$，以地心作为坐标原点，沿地月连线建立$x$轴，在$x$轴上有一个探测器。仅考虑地球和月球对探测器的引力作用，可得探测器引力势能$E_{p}$随位置变化关系如图所示，已知在$x=d$处探测器的引力势能最大，则地球与月球的质量之比为$(\qquad)$

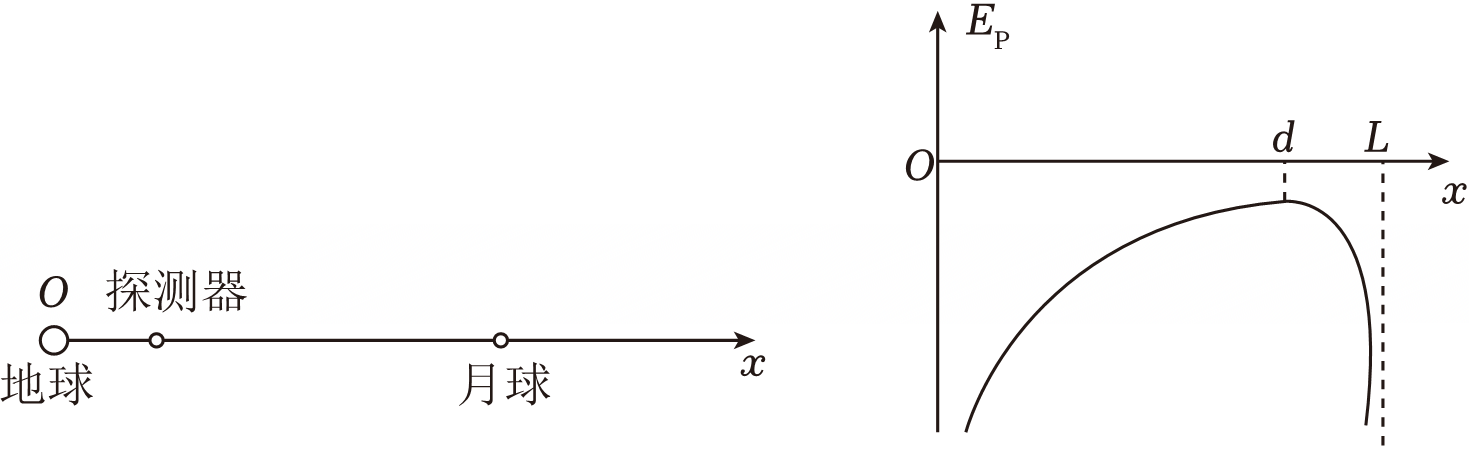
$\\left( \\dfrac{d}{L-d} \\right)^{2}$

$\\left( \\dfrac{L-d}{d} \\right)^{2}$

$\\left( \\dfrac{d}{L+d} \\right)^{2}$

$\\left( \\dfrac{L+d}{d} \\right)^{2}$

设地球质量为$M$，月球的质量为$m$，探测器的质量为$m_{0}$，引力的合力做功与引力势能的关系$F\Delta x=-\Delta E_{p}$，可知$E_{p}-x$图线的切线斜率绝对值为$\left|\dfrac{\Delta E_{p}}{\Delta x}\right|=F$，由图可知，图像切线斜率绝对值先减小后增大，则地球和月球对探测器作用力随探测器位置$x$的增大，先逐渐减小后逐渐增大；在$x=d$处图线的切线斜率为$0$，则探测器在该处受地球和月球的引力的合力为零，即$\dfrac{GMm_{0}}{d^{2}}=G\dfrac{mm_{0}}{(L-d)^{2}}$，可得地球与月球的质量之比为$\dfrac{M}{m}=\left( \dfrac{d}{L-d} \right)^{2}$，故$\rm A$正确，$\rm BCD$错误。

故选：$\rm A$。