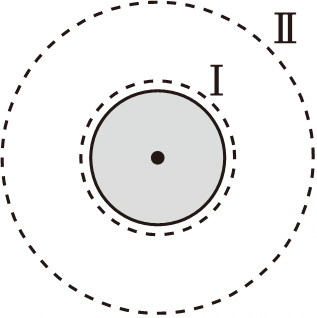
物体在万有引力场中具有的势能叫做引力势能，若取离地球无穷远处的引力势能为零，则质量为$m$的物体引力势能为$E_{P}=-\dfrac{GMm}{r}$，其中$G$为引力常量，$M$为地球的质量，$r$为物体到地心的距离。如图虚线圆为人造地球卫星的两个圆轨道，轨道Ⅰ是近地轨道。已知轨道Ⅱ的半径为轨道Ⅰ的$2$倍，地球半径为$R$，则质量为$m_{0}$的人造地球卫星$(\qquad)$

在轨道Ⅰ上的速率小于在轨道Ⅱ上的速率

在轨道Ⅰ上的周期大于在轨道Ⅱ上的周期

从轨道Ⅰ到轨道Ⅱ克服引力做的功为$\\dfrac{GMm_{0}}{R}$

从轨道Ⅰ到轨道Ⅱ需要的能量至少为$\\dfrac{GMm_{0}}{4R}$

$\rm AB$、设卫星绕地球做圆周运动半径$r$，牛顿第二定律得：$\dfrac{GMm_{0}}{r^{2}}=m_{0}r\dfrac{4\pi^{2}}{T^{2}}=m_{0}\dfrac{v^{2}}{r}$，解得：$v=\sqrt{\dfrac{GM}{r}}$，$T=2\pi\sqrt{\dfrac{r^{3}}{GM}}$，轨道Ⅰ的半径小，所以轨道Ⅰ上卫星的速度大，周期小。故$\rm A$错误，$\rm B$错误；

$\rm C$、从轨道Ⅰ到轨道Ⅱ克服引力做的功为等于引力势能的变化，即：$W= E_{P2}-E_{P1}=- \dfrac{GMm_{0}}{2R}-\left(-\dfrac{GMm_{0}}{R}\right)=\dfrac{GMm_{0}}{2R}$．故$\rm C$错误；

$\rm D$、在$r$轨道上运动具有的动能：$E_{k}=\dfrac{1}{2}m_{0}v^{2}=\dfrac{GMm_{0}}{2r}$，所以卫星在轨道Ⅰ上的机械能为：$E_{1}=E_{k1}+E_{P1}=\dfrac{- GMm_{0}}{2R}$，卫星在轨道Ⅱ上的机械能为：$E_{2}=E_{k2}+E_{P2}=\dfrac{- GMm_{0}}{4R}$

从轨道Ⅰ到轨道Ⅱ需要的能量至少为：$\Delta E=E_{2}-E_{1}=-\dfrac{GMm_{0}}{4R}-\left(-\dfrac{GMm_{0}}{2R}\right)=\dfrac{GMm_{0}}{4R}$。故$\rm D$正确。

故选：$\rm D$。