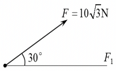
已知一个力$F=10\sqrt{3}\;\rm N$，可分解为两个分力$F_{1}$和$F_{2}$，已知$F_{1}$方向与$F$夹角为$30^\circ$（如图所示），$F_{2}$的大小为$10\;\rm N$，则$F_{1}$的大小可能是$(\qquad)$

$5\\sqrt{3}\\;\\rm N$

$10\\sqrt{3}\\;\\rm N$

$15\\;\\rm N$

$20\\;\\rm N$

已知合力$F=10\sqrt{3}\;\rm N$，$F_{1}$方向与$F$夹角为$30^\circ$，$F_{2}$的大小为$10\;\rm N$，以$F$的箭头处为圆心，以$F_{2}$的大小为半径做圆，则该圆与$F_{1}$的交点即$F_{1}$的大小，

如图，所以

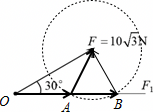
$F_{1}$的长度为$OA$时：$\dfrac{10}{\sin30{^\circ}}=\dfrac{10\sqrt{3}}{\sin\angle OAF}$

所以：$∠OAF=120^\circ$

则：$∠OFA=180^\circ-30^\circ-120^\circ=30^\circ$

所以：$F_{1}=F_{2}=10\;\rm N$

$F_{1}$的长度为$OB$时：$\dfrac{10}{\sin30{^\circ}}=\dfrac{10\sqrt{3}}{\sin\angle OBF}$

所以：$∠OBF=60^\circ$

则：$∠OFA=180^\circ-30^\circ-60^\circ=90^\circ$

所以：$F_{1}= \dfrac{F}{\cos30{^\circ}}=\dfrac{10\sqrt{3}}{\dfrac{\sqrt{3}}{2}} =20\;\rm N$，故$\rm ABC$错误，$\rm D$正确。

故选：$\rm D$。